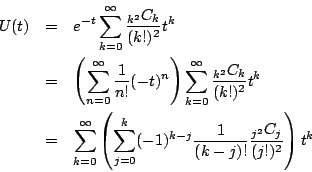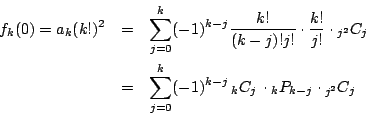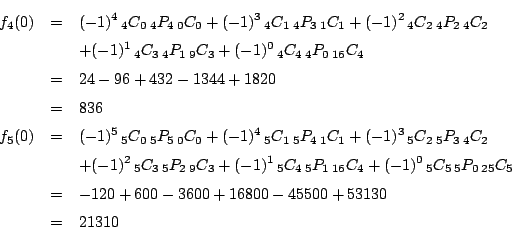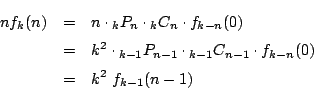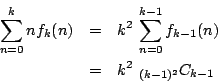次: 素数の分布
上: 生成関数の方法
前: カタラン数の生成関数
南海
まず98年の京大の入試問題と
その一般化を紹介しよう.このときは史織さんが考えてくれた.
例 1.6.3
[98年京大前期文理]
袋に青色,赤色,白色の形の同じ玉がそれぞれ 3 個ずつ入っている.
各色の 3 個の玉にはそれぞれ 1 , 2 , 3 の番号がついている.
これらの 9 個の玉をよくかきまぜて袋から同時に 3 個の玉を取り出す.取り出した 3 個のうちに同
色のものが他になく,同番号のものも他にない玉の個数を得点とする.
たとえば,青1番,赤1番,白3番を取り出したときの得点は 1 で,青2番,赤2番,赤3番を
取り出したときの得点は 0 である。このとき以下の問に答えよ.
- 得点が
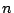 になるような取り出し方の数を
になるような取り出し方の数を 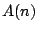 とするとき,
とするとき,
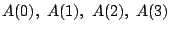 を求めよ.
を求めよ.
- 得点の期待値を求めよ.
例 1.6.4 (問題の一般化)
袋に, 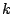 種の色でぬられた同じ形の玉が
種の色でぬられた同じ形の玉が 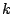 個ずつ
個ずつ 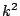 個入っている.
各色の
個入っている.
各色の 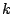 個の玉には 1 から
個の玉には 1 から 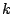 まで番号がついている.ここから同時に
まで番号がついている.ここから同時に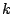 個の玉を取り出す.
個の玉を取り出す.
史織 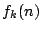 は
は
- まず
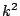 個の中から一つ選ぶ.
次に最初に選ばれたものと色か番号が一致するものを除いた
個の中から一つ選ぶ.
次に最初に選ばれたものと色か番号が一致するものを除いた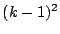 個の中から
一つとる.以下
個の中から
一つとる.以下 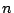 個目を
個目を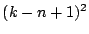 個から一つ選ぶまでとる.
この
個から一つ選ぶまでとる.
この 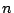 個の取り方は,取り出す順序に関係ないから
個の取り方は,取り出す順序に関係ないから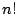 で割って,
で割って,
- 残る k-n 個は互いに同色同番があるような選び方だから,
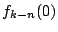 通り.
通り.
- よって,
である.すべての選び方は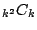 通りだから,
通りだから, の漸化式
の漸化式
が成り立つ.最初の条件は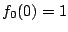 である.
である.
史織
ところで,この漸化式は解けるのですか.
南海
それが問題だ.少しでも前進しなければならない.
できているところまで話そう.

である.つまり,

ここで,
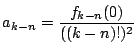 と置こう.
そして次の二つの無限級数を考える.
と置こう.
そして次の二つの無限級数を考える.
すると
である.漸化式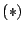 はこれが
はこれが
となることを意味している.
ところが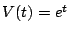 で,さらに
で,さらに
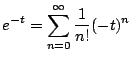 あるから,
あるから,
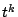 の係数を比較して,
の係数を比較して,
史織
わー,解けてる.ためしてみます.
南海
期待値は求まる.
である.ゆえに
したがって求める期待値は
である.
南海
これが生成関数の方法で,
数列を求めるのに大変強力な方法なのだ.
この先は,上に現れた関数の満たす関係を求めなければならず,それはできていない.
京大の問題は生成関数まで使わせてくれたという意味で大変良い問題だった.



次: 素数の分布
上: 生成関数の方法
前: カタラン数の生成関数
Aozora Gakuen
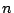 になるような取り出し方の数を
になるような取り出し方の数を 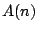 とするとき,
とするとき,
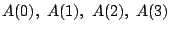 を求めよ.
を求めよ.
 の漸化式
の漸化式
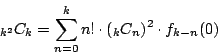


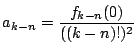 と置こう.
そして次の二つの無限級数を考える.
と置こう.
そして次の二つの無限級数を考える.
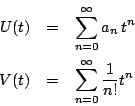
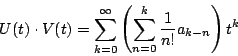
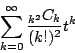
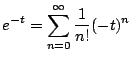 あるから,
あるから,