 南海
それでは,懸垂線の方程式を求め,その関数に関するいくつかの話題を考えていこう.
ちょうど鎖があるので吊してみよう.
この曲線を懸垂線、英語では Catenary という. Catenary という言葉は1691年にホイヘンス(Huygens)に
よって作られたそうである.
語源はラテン語の鎖 "catena"で,英語の鎖 chain も源をたどれば同じ語源に行き着く.
南海
それでは,懸垂線の方程式を求め,その関数に関するいくつかの話題を考えていこう.
ちょうど鎖があるので吊してみよう.
この曲線を懸垂線、英語では Catenary という. Catenary という言葉は1691年にホイヘンス(Huygens)に
よって作られたそうである.
語源はラテン語の鎖 "catena"で,英語の鎖 chain も源をたどれば同じ語源に行き着く.
 南海
それでは,懸垂線の方程式を求め,その関数に関するいくつかの話題を考えていこう.
ちょうど鎖があるので吊してみよう.
この曲線を懸垂線、英語では Catenary という. Catenary という言葉は1691年にホイヘンス(Huygens)に
よって作られたそうである.
語源はラテン語の鎖 "catena"で,英語の鎖 chain も源をたどれば同じ語源に行き着く.
南海
それでは,懸垂線の方程式を求め,その関数に関するいくつかの話題を考えていこう.
ちょうど鎖があるので吊してみよう.
この曲線を懸垂線、英語では Catenary という. Catenary という言葉は1691年にホイヘンス(Huygens)に
よって作られたそうである.
語源はラテン語の鎖 "catena"で,英語の鎖 chain も源をたどれば同じ語源に行き着く.
耕一
放物線と似ていますが,放物線とは違うのですね.
 南海
違う.二つを同じ座標平面にかいてみよう.太い方が懸垂線,細い方が放物線だ.
さすがに懸垂線は指数関数でできているだけに,はじめは放物線より値が小さいが,
その後はずっと大きい値をとる.
南海
違う.二つを同じ座標平面にかいてみよう.太い方が懸垂線,細い方が放物線だ.
さすがに懸垂線は指数関数でできているだけに,はじめは放物線より値が小さいが,
その後はずっと大きい値をとる.
問題はこの懸垂線の式を求めるということだった.
つまり求める曲線を![]() とおき,
とおき,![]() を決定しようということだ.懸垂線の意味から
この曲線が
を決定しようということだ.懸垂線の意味から
この曲線が![]() 軸に関して対称であるとしてよい.また,
軸に関して対称であるとしてよい.また,
任意の![]() に対して,曲線の原点と
に対して,曲線の原点と![]() までの部分を写真のように赤線に引く.
この部分の力の釣り合いを考えよう.
までの部分を写真のように赤線に引く.
この部分の力の釣り合いを考えよう.
南海
原点では左方向に一定の張力が働く.この大きさを![]() とする.これは定数である.
そこで,図のように任意の
とする.これは定数である.
そこで,図のように任意の![]() に対して,点
に対して,点![]() で接線方向に大きさ
で接線方向に大きさ![]() の
張力が働いているとする.この大きさはもちろん
の
張力が働いているとする.この大きさはもちろん![]() によって変化する.
によって変化する.
 鎖には重力が作用している.鎖の重みと張力とが釣り合っている,と考えられる.
鎖には重力が作用している.鎖の重みと張力とが釣り合っている,と考えられる.
原点での張力,原点から![]() までの鎖に働く重力,点
までの鎖に働く重力,点![]() での接線方向の張力,
これらが釣り合っている.点
での接線方向の張力,
これらが釣り合っている.点![]() での接線方向が
での接線方向が![]() 軸の正の方向となす角を
軸の正の方向となす角を
![]() とおこう.
とおこう.
張力を![]() 軸方向と
軸方向と![]() 軸方向に分解する.
軸方向に分解する.
![]() 軸方向は
軸方向は![]() と
と![]() とが釣り合っている.
とが釣り合っている.
![]() 軸方向について考える.図の赤線部分の長さ
軸方向について考える.図の赤線部分の長さ![]()
ここで, とおこう.するとすべてを決定している関係式は次の3つである.
とおこう.するとすべてを決定している関係式は次の3つである.

![]() の両辺を
の両辺を![]() で微分する.
で微分する.
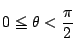 なので
なので![]() を代入して
を代入して
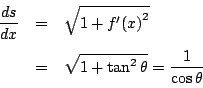
![]() の両辺を
の両辺を![]() で微分する.
で微分する.
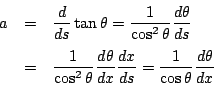
これを![]() について0から
について0から![]() まで積分すると
まで積分すると
南海
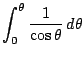 は計算できるか.
は計算できるか.
耕一 はい.

南海
両辺の逆数をとると
耕一
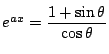 なので
なので
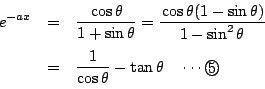
南海
![]() の辺々を引いて,
の辺々を引いて,
変数を![]() にして両辺0から
にして両辺0から![]() まで積分する.
まで積分する.![]() なので
なので
![\begin{eqnarray*}
\left[f(t)\right]_0^x&=&\int_0^x\dfrac{e^{at}-e^{-at}}{2}\,dt\\
∴&&f(x)=\dfrac{e^{ax}+e^{-ax}}{2a}-\dfrac{1}{a}
\end{eqnarray*}](images/img1093.png)
南海
今は![]() にしたが,
にしたが,![]() で,
で,![]() のものが懸垂線の標準的なものだ.
つまり
のものが懸垂線の標準的なものだ.
つまり
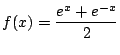 だ.
だ.
耕一
計算では途中で媒介変数![]() がうまく使われています.
がうまく使われています.
南海 曲線の長さを媒介変数にとると計算が簡明になるというのは, 微分幾何という分野では基本的なことなのだが高校数学では難しい. この考えを用いた入試問題を一つ紹介しよう.
放物線
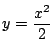 のうち,
のうち,![]() の部分を
の部分を![]() とする.
とする.![]() 上の点
上の点
![]() に対し,原点
に対し,原点![]() から
から![]() までの
までの![]() の部分の長さを
の部分の長さを
![]() で表す.
で表す.![]() と
と![]() を
を![]() の関数とみなして
の関数とみなして
![]() とおくとき,以下の問に答えよ.
とおくとき,以下の問に答えよ.
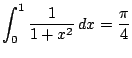 を用いてもよい.
を用いてもよい.