![]() のなかに同じものがればそれをまとめれば,再び重み付き平均
になる.したがって
のなかに同じものがればそれをまとめれば,再び重み付き平均
になる.したがって
![]() はすべて異なり必要なら並べ替えて小さい
方から順にならんでいるとしてよい.
はすべて異なり必要なら並べ替えて小さい
方から順にならんでいるとしてよい.
![]() とする.
とする.
なので,
定理6から![]() 個の点
個の点
でできる
さらに
![]() とすると,
とすると, ![]() である.
である.
とおくと,
である.ゆえに定理1から
は
つまり

が示された.
![]() のなかに同じものがればそれをまとめれば,再び重み付き平均
になる.したがって
のなかに同じものがればそれをまとめれば,再び重み付き平均
になる.したがって
![]() はすべて異なり必要なら並べ替えて小さい
方から順にならんでいるとしてよい.
はすべて異なり必要なら並べ替えて小さい
方から順にならんでいるとしてよい.
![]() とする.
とする.
定理6から![]() 個の点
個の点
さらに
![]() とすると,
とすると, ![]() である.
である.



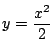 より
より


つまり

したがって

曲線の方程式は ![]() なので,この曲線は
なので,この曲線は![]() 座標では媒介変数
座標では媒介変数![]() によって
によって
ここで

したがって求める長さを ![]() とすると
とすると

 なので
なので
![\begin{eqnarray*}
l&=&\pi\sqrt{1+\pi^2}-l+ \left[\log(\theta+\sqrt{1+\theta^2})...
...ht]_0^{\pi}\\
&=&\pi\sqrt{1+\pi^2}-l+\log(\pi+\sqrt{1+\pi^2})
\end{eqnarray*}](images/img1382.png)
別解
1の計算は
![]() と変数変換してもよい.
と変数変換してもよい.
このとき
![]() なので,
なので,
![]() となる.
となる.
また(1)から
 ,つまり
,つまり
![]()
積分域は
![]() となるので
となるので
![]() とおく.
とおく.


