

 次: ζを関・ベルヌーイ数で表す
上: ζを関・ベルヌーイ数で表す
前: 倍角公式から得られる代数方程式
次: ζを関・ベルヌーイ数で表す
上: ζを関・ベルヌーイ数で表す
前: 倍角公式から得られる代数方程式
以上の準備のもとで以下の定理を示す.
定理 1
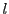
を自然数とする.
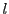
に対して自然数
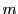
を十分大きくとる.
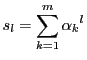
は
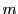
の
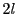
次多項式であり,最高次の係数
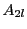
は
である.
■
証明
数学的帰納法で示す.
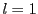 のとき.
のとき.
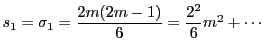 である.
ここで,
である.
ここで,
なので成立している.
定理の命題が
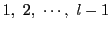 で成立しているとする.
で成立しているとする.
補題1の項
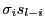 ,
,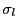 において,
において,
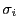 は
は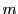 の
の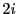 次多項式であり,
次多項式であり,
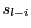 は
は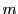 の
の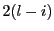 次多項式であるから,
次多項式であるから,
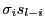 は
は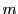 の
の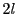 次多項式である.
次多項式である.
帰納法の仮定から
の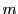 の
の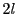 次の係数
次の係数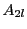 は
は
となる.これを変形整理する.
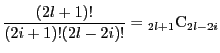 より
より
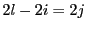 とおくと
とおくと
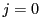 のときの項
のときの項
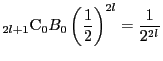 と
と
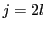 のときの項
のときの項
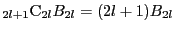 を加減して
を加減して
3以上の奇数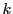 に対して
に対して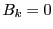 で上記の形式の和で項
で上記の形式の和で項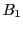 に対応するのは
に対応するのは
である.よってこれらの項を加減し,和を2でくくると
を得る.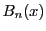 の定義から
の定義から
である.よって
である.命題3の3.より
なので
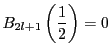 である.
この結果
である.
この結果
となる.
定理の命題は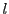 のときにも成立し,すべての自然数
のときにも成立し,すべての自然数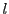 に対して成立する.
□
に対して成立する.
□
Aozora
2018-05-14
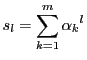 は
は
![]() のとき.
のとき.
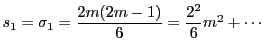 である.
ここで,
である.
ここで,
![]() で成立しているとする.
で成立しているとする.
![]() ,
,![]() において,
において,
![]() は
は![]() の
の![]() 次多項式であり,
次多項式であり,
![]() は
は![]() の
の![]() 次多項式であるから,
次多項式であるから,
![]() は
は![]() の
の![]() 次多項式である.
次多項式である.
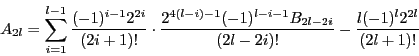
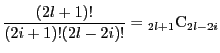 より
より
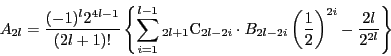
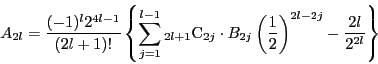
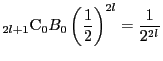 と
と
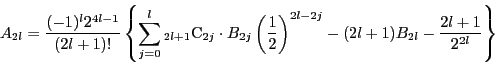
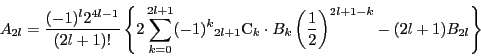
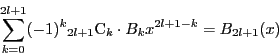
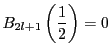 である.
この結果
である.
この結果