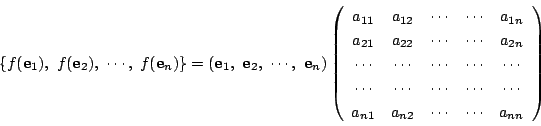次: 線型写像の演算と行列の演算 上: 線型写像と行列 前: 線型写像と行列

線型写像の行列表現

南海　 ベクトル空間$V$と一組の基底

$$\mathrm{\bf e}_1,\ \mathrm{\bf e}_2,\ \cdots,\ \mathrm{\bf e}_n$$

をとり， $V$から$V$への線型写像$f$を考える． $V$から他のベクトル空間でもよいが，結局は$V$から$V$への場合を考えれば， 他の場合は処理できるので，ここでは過度な一般化は避け， $V$から$V$への線型写像を考えよう．

$V$のベクトル $\mathrm{\bf u}$を実数 $x_1,\ x_2,\ \cdots,\ x_n$を用いて

$$\mathrm{\bf u}=\sum_{k=1}^nx_k\mathrm{\bf e}_k$$

と表す．

$$f(\mathrm{\bf u})= f\left(\sum_{k=1}^nx_k\mathrm{\bf e}_k \right) =\sum_{k=1}^nx_kf(\mathrm{\bf e}_k)$$

である．よって $k=1,\ 2,\ 3,\ \cdots,\ n$について $f(\mathrm{\bf e}_k)$がわかれば， $f(\mathrm{\bf u})$が決まる．

$$\begin{eqnarray*} f(\mathrm{\bf e}_1)&=& a_{11}\mathrm{\bf e}_1+a_{21}\mathrm{\b... ...rm{\bf e}_1+a_{2n}\mathrm{\bf e}_2+\cdots+a_{nn}\mathrm{\bf e}_n \end{eqnarray*}$$

とおく．

耕一　 係数のつきかたが行列の成分の並び方と逆ですね．

南海　 そうだ．こうすることで以下に見るように統一的に扱える． まず，

$$\begin{eqnarray*} f(\mathrm{\bf u})&=&\sum_{k=1}^nx_kf(\mathrm{\bf e}_k) =\sum_{... ...\sum_{j=1}^n\left(\sum_{k=1}^na_{jk}x_k\right) \mathrm{\bf e}_j \end{eqnarray*}$$

となる．ここで，

$$\begin{eqnarray*} y_1&=&a_{11}x_1+a_{12}x_2+\cdots a_{1n}x_n\\ y_2&=&a_{21}x_1+... ...2n}x_n\\ &&\cdots\\ y_n&=&a_{n1}x_1+a_{n2}x_2+\cdots a_{nn}x_n \end{eqnarray*}$$

とおく．すると，

$$f(\mathrm{\bf u})=\sum_{j=1}^n y_j\mathrm{\bf e}_j$$

となる．この $x_1,\ x_2,\ \cdots,\ x_n$と $y_1,\ y_2,\ \cdots,\ y_n$ の関係を高校数学Cの行列の積の記法で書けば，

$$\left( \begin{array}{c} y_1\\ y_2\\ \cdots\\ \cdots\... ... x_1\\ x_2\\ \cdots\\ \cdots\\ x_n \end{array}\right)$$

となる．

耕一　 写像$f$による基底の行き先を元の基底を用いて表す行列の係数を， $a_{11}$から$a_{nn}$への対角線に関して対称に入れ替えた行列が， 通常の行列による一次変換の記法に一致するのですね．

南海　 そうだ．

耕一　 高校数学Cで成分で書かれたベクトルと行列によって， 一次変換が定まると習いました． 実は逆で， 線型写像に対して基底をひとつ固定することで，行列が定まるのですね．

南海　 ここで，基底の像と行列の関係を見やすくするために次のように考えよう． 基底を一組固定し，それを

$$\left( \mathrm{\bf e}_1,\ \mathrm{\bf e}_2,\ \cdots,\ \mathrm{\bf e}_n \right)$$

のように書く． この基底で表されるベクトル

$$\mathrm{\bf u}=\sum_{k=1}^nx_k\mathrm{\bf e}_k$$

を

$$\mathrm{\bf u}=\left( \mathrm{\bf e}_1,\ \mathrm{\bf e}_2,\ ... ... x_1\\ x_2\\ \cdots\\ \cdots\\ x_n \end{array}\right)$$

と表すことにする．

耕一　 内積の計算と同じようにかけて和をとるのですね．

南海　 これを用いると，これらの基底の$f$による像は

$$\left\{ f(\mathrm{\bf e}_1),\ f(\mathrm{\bf e}_2),\ \cdots,\... ...ots\\ a_{n1}&a_{n2}&\cdots&\cdots&a_{nn} \end{array}\right)$$

と表せる．このとき

$$\begin{eqnarray*} f\left(\mathrm{\bf u}\right) &=&\left\{ f(\mathrm{\bf e}_1),\ ... ...} x_1\\ x_2\\ \cdots\\ \cdots\\ x_n \end{array}\right) \end{eqnarray*}$$

となる．これが

$$\left( \mathrm{\bf e}_1,\ \mathrm{\bf e}_2,\ \cdots,\ \mathr... ... y_1\\ y_2\\ \cdots\\ \cdots\\ y_n \end{array}\right)$$

となるのだから，

$$\left( \begin{array}{c} y_1\\ y_2\\ \cdots\\ \cdots\... ... x_1\\ x_2\\ \cdots\\ \cdots\\ x_n \end{array}\right)$$

となるのだ．