


次: 逆行列の存在条件
上: 線型写像と行列
前: 線型写像の行列表現
南海
基底
 を固定し,
線型写像
を固定し,
線型写像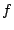 から定まる行列
から定まる行列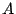 を
を のように書くことにしよう.
2つの線型写像
のように書くことにしよう.
2つの線型写像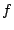 と
と ,および実数
,および実数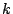 に対して
に対して
と定めれば,写像の和と実数倍が定義される.
耕一
ということはベクトル空間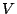 から
から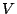 への線型写像の集合自体が,
またベクトル空間になるということですか.
への線型写像の集合自体が,
またベクトル空間になるということですか.
南海
その通りなのだ.
が,ここではこの線型写像の作るベクトル空間の研究には深入りしない.
ここでは上に定めた線型写像の和と実数倍に対して,
対応する行列もまた,行列の和と実数倍
になることである.つまり
が成り立つ.これはすぐにわかる.
さらに写像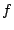 と
と の積
の積 を,写像の合成によって
を,写像の合成によって
で定める.
このとき
が成り立つ,ただし右辺は行列の積である.
耕一
確認します.
基底を
 とし,
とし,
とします.つまり行列の一般項で書くと
とします.
このとき,
よって
とおくと
となり,確かに数学Cで習った行列の積に一致します.つまり
となっています.
南海
これは
より
なので
が成立する.このようにしてもわかる.
Aozora Gakuen


![]() から
から![]() への線型写像の集合自体が,
またベクトル空間になるということですか.
への線型写像の集合自体が,
またベクトル空間になるということですか.

![]() とし,
とし,


