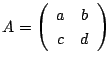 に対して,
に対して,
耕一 高校の数学でも行列式は出ているのですか.
南海 行列式という名前は出てこない.
だが,行列
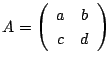 に対して,
に対して,
耕一
はい.
![]() が0でないことが,
が0でないことが,
![]() の逆行列が存在するための必要十分条件でした.
の逆行列が存在するための必要十分条件でした.
南海
この![]() が行列
が行列![]() の行列式なのだ.
の行列式なのだ.
![]() の行列式であることを明示して
の行列式であることを明示して
![]() と書いたり,
もとの行列の各成分で明示して
と書いたり,
もとの行列の各成分で明示して

耕一
まえから不思議に思っていたのですが,
行列
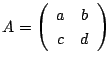 を2つの縦ベクトル
を2つの縦ベクトル

南海
じつはここに線型写像と行列式の内容が隠れている.
ベクトル空間と![]() 座標の関係は後に改めて考える.
例を,高校数学で習う
座標の関係は後に改めて考える.
例を,高校数学で習う![]() 平面上のベクトルにとって,説明しよう.
平面上のベクトルにとって,説明しよう.
![]() 平面上のベクトルは,始点を原点にとることで,
平面上のベクトルは,始点を原点にとることで,![]() 座標で表すことができた.
これを
座標で表すことができた.
これを


ある線型写像![]() をとる.
この基底に対して線型写像
をとる.
この基底に対して線型写像![]() で定まる行列が
で定まる行列が
 であるとする.
これは何を意味していたか.
であるとする.
これは何を意味していたか.
耕一
基底が線型写像![]() によって
によって

南海 うん. そうすることで, 二次の場合の自然な線型写像と行列の対応の一般化になるのだ.
さて,一般の場合の行列式を定義するために,
二次の行列式の性質をいくつかまとめておこう.
行列
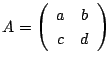 を二つの縦ベクトル
を二つの縦ベクトル

耕一 最初の二つは左側のベクトルに関して線型であることを意味しています. 第三の性質から右側の成分に関しても線型です.
![]() と
と
![]() が一次独立でないとき,
つまり
が一次独立でないとき,
つまり
![]() のとき,
行列式が0になることがここから導かれればいいのですが.
のとき,
行列式が0になることがここから導かれればいいのですが.
南海
第三の性質から
耕一
だから