をとる.
に対し,次の性質をもつ実数
がただひとつ定まる.
-
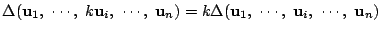 .
.
-
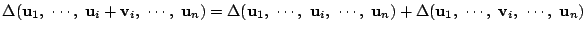 .
.
-
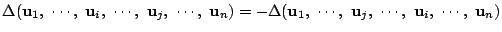 .
.
-
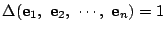
耕一 証明は難しいのですか.
南海
いや.実際に構成してみせるのだ.
ただそのために置換の考え方がいる.
![]() 個の数
個の数
![]() の集合
の集合
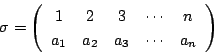
また
![]() のうち
のうち![]() と
と![]() のみを入れ替え,他はそのままである置換を互換といい,
のみを入れ替え,他はそのままである置換を互換といい,
![]() のように書きあらわす.つまり
のように書きあらわす.つまり
耕一
![]() のときは,置換は結局
のときは,置換は結局
![]() の決め方だから
の決め方だから![]() 個あるのですね.
個あるのですね.
 南海
置換を目で見るには次のようにしてみればよい.例えば
南海
置換を目で見るには次のようにしてみればよい.例えば
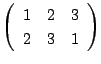 は,次のようにひもで結べばよい.
は,次のようにひもで結べばよい.
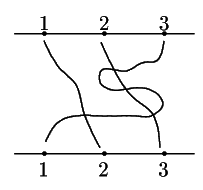
耕一 ひもは2回交わります.
南海 そこでどのようなことが起こっているか.
耕一
まず2と3が入れ替わり,次にその2と1が入れ替わります.
実際上から順にこの入れ替えを書くと

南海
こうして置換
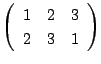 は2つの互換
は2つの互換
![]() の積になった.
の積になった.
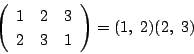
 耕一
でも
右のようなときもあります.これは
耕一
でも
右のようなときもあります.これは
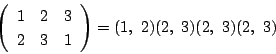
南海 次の事実が成り立つ.
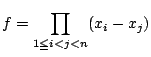 とおく.
とおく.
![]() 個の文字の置換
個の文字の置換![]() によって,
によって,
![]() を置きかえると,
新しい
を置きかえると,
新しい![]() ができるが,
ができるが,
![]() は
は![]() の符号のみをかえるので,
の符号のみをかえるので,
![]() であり,
その符号は
であり,
その符号は![]() によって確定する.
一方,置換が偶数個の互換の積に分解されるなら
によって確定する.
一方,置換が偶数個の互換の積に分解されるなら![]() ,
奇数個の互換の積に分解されるなら,
,
奇数個の互換の積に分解されるなら,![]() である.
したがって,偶数奇数の別は分解の仕方によらない.
□
である.
したがって,偶数奇数の別は分解の仕方によらない.
□
偶数個の互換の積に分解される置換を偶置換,
奇数個の互換の積に分解される置換を奇置換という.
記号で
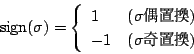
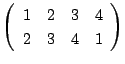 は
は
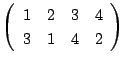 は
は
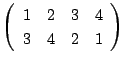 は
は
南海 定理4の証明をしておこう. ある程度添え字の置き方にも慣れてきたので和記号を用いていく.
定理 4 の証明
定理 4 に掲げた4つの性質をもつ![]() が存在するとする.
が存在するとする.
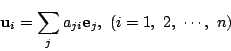
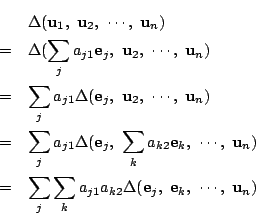
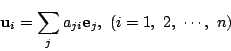
さて行列
![]() に対して,この基底に関して
に対して,この基底に関して
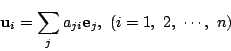
したがって
![]() の
の
![]() に,
に,
![]() 以外のベクトルの1次結合を加えても,
行列式の値は変わらない.
実際
以外のベクトルの1次結合を加えても,
行列式の値は変わらない.
実際
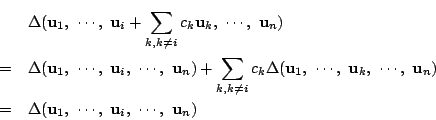
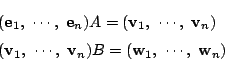
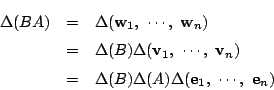
![]() なら,まず
なら,まず
![]() は1次従属.その関係式に
は1次従属.その関係式に
![]() のときも成立する.
のときも成立する.
耕一 今は行列を縦ベクトルに分けて,行列式を定義しましたが,横ベクトルに分けてもいいのですか.
南海
それは,![]() の逆置換
の逆置換![]() ,置換群的な考察が必要なのだ.
,置換群的な考察が必要なのだ.
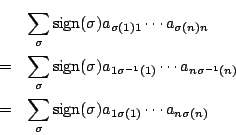
耕一 少し難しいです.
南海
そうだろう.そこで具体的な場合に戻ろう.
2次行列の場合,この定義が![]() そのものであることを確認してほしい.
ただし,
基底は
そのものであることを確認してほしい.
ただし,
基底は
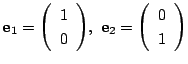 とする.
とする.
耕一
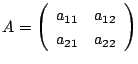 とすると,
とすると,
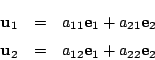
1と2の置換は
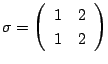 と
と
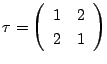 の2つです.
の2つです.
![]() なので
なので
南海
3次の場合は?
ただし,
基底は
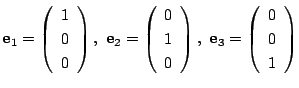 とする.
とする.
耕一 同じように考えます.
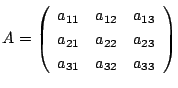 とする.
とする.
1,2,3の置換は,![]() を並べ替えた結果で書くと
を並べ替えた結果で書くと
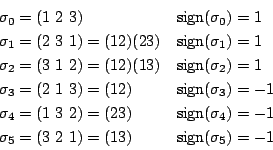
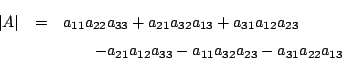
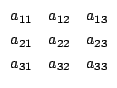 で,
左上から右下方向にとるときは符号は正,
左下から右上方向にとるときは符号は負ということで,覚えやすい.
で,
左上から右下方向にとるときは符号は正,
左下から右上方向にとるときは符号は負ということで,覚えやすい.