
 次: 三項間漸化式を解く
上: 三項間漸化式と行列の累乗
次: 三項間漸化式を解く
上: 三項間漸化式と行列の累乗
拓生 定期テストで,三項間漸化式
を解く問題が出ました.
特性方程式 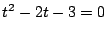 の二つの解が
の二つの解が 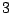 と
と 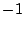 で異なります.
特性方程式の異なる二つの解が
で異なります.
特性方程式の異なる二つの解が
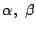 のとき
のとき
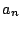 がいつも
がいつも
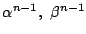 からできているので,求める数列を
からできているので,求める数列を
と置いて,最初の二項が一致するように 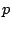 と
と 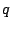 を求めました.
でも試験では大幅に減点でした.
を求めました.
でも試験では大幅に減点でした.
南海 数列がいつもこの形をしていることに気づいたのはよい.
しかしただ単に計算だけするのは解答としては不十分だ.
このように書けることはどんな意味があるのか考え,
なぜこの形になるのか論証しなければならない.
拓生 もう一つ質問ですが,連立漸化式
を解こうとしていろいろやっていると,
が得られました.その変形はいつもできそうですが,
連立漸化式と三項間漸化式の関係がはっきりしていません.
南海 なるほど.それならこの機会に
三項間漸化式と連立漸化式についてまとめておこう.
まず三項間漸化式と連立二項間漸化式の相互関係だ.
数列 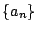 と
と 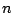 の関数
の関数 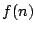 があってその間に
があってその間に
の関係式がすべての 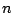 に対して成り立つとき,この関係式を三項間漸化式という.
に対して成り立つとき,この関係式を三項間漸化式という.
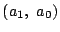 の値が決まれば,数学的帰納法によって数列
の値が決まれば,数学的帰納法によって数列 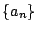 の各項の値が一意に定まる.
の各項の値が一意に定まる.
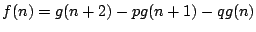 となる0以上の整数を定義域とする関数
となる0以上の整数を定義域とする関数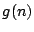 が見つかれば,これは
が見つかれば,これは
となる.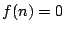 の場合に解けることが,基本だ.
それで以下では
の場合に解けることが,基本だ.
それで以下では
となる漸化式を考えよう.
次に,二つの数列 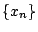 と
と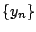 の間に成り立つ
の間に成り立つ
のような漸化式を連立二項間漸化式という.
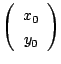 の値が定まれば,
二つの数列
の値が定まれば,
二つの数列
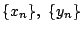 の各項の値が一意に定まる.
の各項の値が一意に定まる.
この二つの形の漸化式は,実は同等である.つまり一方から他方への変換があり,
それによって,一方が解ければ他方が解ける.
まず,連立二項間漸化式2を考えよう.
行列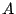 を
を
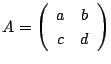 とすると2は
とすると2は
と表される.したがって,等比数列と同様に
となる.
ハミルトン・ケイレイの定理より
つまり
である.これからまた
つまり, 数列 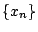 と
と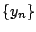 はともに同じ三項間漸化式をみたす.
はともに同じ三項間漸化式をみたす.
をみたす.
このとき,それぞれの三項間漸化式の初期条件は
である.
こんどは三項間漸化式1を考えよう.
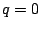 なら実質は二項間等比数列なので
なら実質は二項間等比数列なので 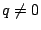 とする.
とする.
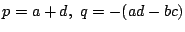 となるような数
となるような数 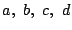 を一組とる.
同じ理由で
を一組とる.
同じ理由で 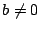 にとる.
その組に対して
にとる.
その組に対して
とおく.
初期条件は
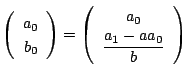 とする.
これは
とする.
これは
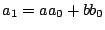 であるように
であるように 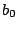 をとるということである.
行列
をとるということである.
行列
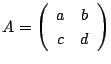 とおくと
とおくと
となる.
ゆえに,この連立二項間漸化式から三項間漸化式を作る方法で作り直した数列 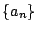 はもとの三項間漸化式1の解になる.
なお数列
はもとの三項間漸化式1の解になる.
なお数列 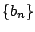 の方は
の方は 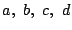 の取り方で異なる.
実際に解くときは
の取り方で異なる.
実際に解くときは
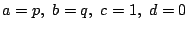 という組を用いればよい.つまり
という組を用いればよい.つまり
とおく.初期条件は
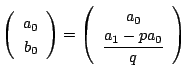 である.
である.
以上から,三項間漸化式を解くことと連立二項間漸化式を解くことは同等である.

 次: 三項間漸化式を解く
上: 三項間漸化式と行列の累乗
Aozora Gakuen
次: 三項間漸化式を解く
上: 三項間漸化式と行列の累乗
Aozora Gakuen

![]() と
と ![]() の関数
の関数 ![]() があってその間に
があってその間に
![]() と
と![]() の間に成り立つ
の間に成り立つ
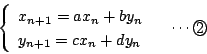
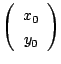 の値が定まれば,
二つの数列
の値が定まれば,
二つの数列
![]() を
を
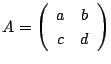 とすると2は
とすると2は
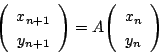
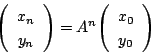
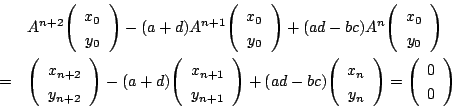
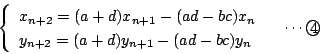
![]() なら実質は二項間等比数列なので
なら実質は二項間等比数列なので ![]() とする.
とする.
![]() となるような数
となるような数 ![]() を一組とる.
同じ理由で
を一組とる.
同じ理由で ![]() にとる.
その組に対して
にとる.
その組に対して
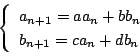
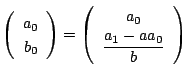 とする.
これは
とする.
これは
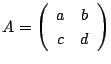 とおくと
とおくと
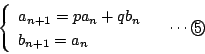
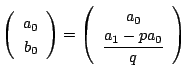 である.
である.