![]() を2次式とする.整式
を2次式とする.整式![]() は
は![]() では割り切れないが,
では割り切れないが,
![]() は
は![]() で割り切れるという.
このとき2次方程式
で割り切れるという.
このとき2次方程式![]() は重解を持つことを示せ.
は重解を持つことを示せ.
解1
![]() は2次式なので,
整式
は2次式なので,
整式![]() を
を![]() で割った余りは1次以下の整式である.
商を
で割った余りは1次以下の整式である.
商を![]() ,余りを
,余りを![]() とする.
とする.
![]() は
は![]() で割り切れないので右辺は定数0ではない.
つまり
で割り切れないので右辺は定数0ではない.
つまり![]() である.よって
である.よって![]() は
は
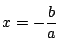 を持つ.□
を持つ.□
解2
![]() の解を
の解を![]() と
と![]() とし,
とし,
このとき![]() と
と![]() は互いに素である.
よって任意の整式
は互いに素である.
よって任意の整式![]() について
について![]() が
が![]() で割りきれることと,
で割りきれることと,
![]() が
が![]() で割り切れかつ
で割り切れかつ![]() で割り切れることが同値である.
で割り切れることが同値である.
もし![]() が因数
が因数![]() をもたなければ,
整式における素因数分解の一意性によって,
をもたなければ,
整式における素因数分解の一意性によって,
![]() も因数
も因数![]() をもたない.
よってもし
をもたない.
よってもし![]() が因数
が因数![]() をもてば,
をもてば,
![]() が因数
が因数![]() をもつ.
をもつ.
![]() は
は![]() で割り切れるので,
で割り切れるので,
![]() が因数
が因数![]() と
と![]() をもち,
その結果
をもち,
その結果![]() が因数
が因数![]() と
と![]() をもつ.
をもつ.
ところがこれは![]() が
が![]() で割りきれることを意味し,仮定と矛盾する.
よって
で割りきれることを意味し,仮定と矛盾する.
よって![]() であり,2次方程式
であり,2次方程式![]() は
は![]() を重解にもつ.
□
を重解にもつ.
□