

 次: 整式の決定[00お茶の水大]
上: 整式と見るか整数と見るか
前: 2次方程式[06京大文理1番]
次: 整式の決定[00お茶の水大]
上: 整式と見るか整数と見るか
前: 2次方程式[06京大文理1番]
問題
1次式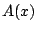 ,
,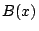 ,
,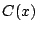 に対して
に対して
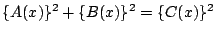 が成り立つとする.
このとき
が成り立つとする.
このとき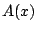 と
と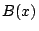 はともに
はともに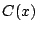 の定数倍であることを示せ.
の定数倍であることを示せ.
解1
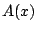 と
と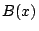 を
を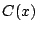 で割った商と余りをそれぞれ
で割った商と余りをそれぞれ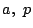 と
と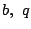 とし,
とし,
とおく.それぞれ1次式であるので,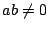 である.
である.
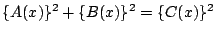 より
より
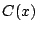 を
を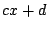 とすると,
とすると,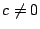 で,両辺の
で,両辺の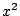 の係数の比較より
の係数の比較より
これから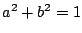 である.
である.
このとき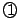 は
は
となる.両辺の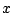 の係数比較から
の係数比較から
その結果,
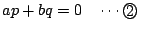 となり,さらに
となり,さらに
である.ここで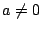 なので
なので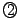 から
から
これを に代入して
に代入して
よって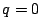 となり,
となり,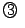 から
から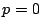 .
.
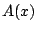 と
と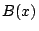 はともに
はともに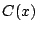 の定数倍であることが示された.□
の定数倍であることが示された.□
解2
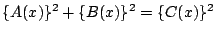 より
より
である.
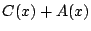 も
も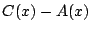 も1次以下の整式であるから
も1次以下の整式であるから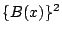 の定数倍になることはない.
の定数倍になることはない.
したがって定数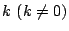 が存在して
が存在して
と表される.
これから
である.
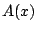 も
も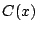 も1次式なので
も1次式なので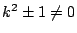 である.
である.
となり,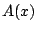 と
と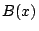 はともに
はともに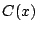 の定数倍であることが示された.
□
の定数倍であることが示された.
□
Aozora Gakuen
![]() ,
,![]() ,
,![]() に対して
に対して
![]() が成り立つとする.
このとき
が成り立つとする.
このとき![]() と
と![]() はともに
はともに![]() の定数倍であることを示せ.
の定数倍であることを示せ.
![]() と
と![]() を
を![]() で割った商と余りをそれぞれ
で割った商と余りをそれぞれ![]() と
と![]() とし,
とし,
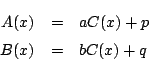
![]() より
より
![]() は
は
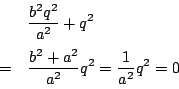
![]() より
より
![]() も
も![]() も1次以下の整式であるから
も1次以下の整式であるから![]() の定数倍になることはない.
の定数倍になることはない.
![]() が存在して
が存在して
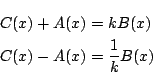
![]() も
も![]() も1次式なので
も1次式なので![]() である.
である.