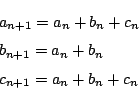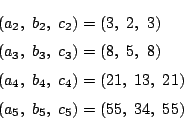3種類の文字a,b,c のなかから重複を許して5個の文字を選び,
横一列に並べてできる文字列をワードと呼ぶ.文字列![]() を含まないワードの総数を求めよ.
を含まないワードの総数を求めよ.
方針
解1
各位置の文字の決め方が3通りあるので,5文字の場合総数は![]() 個ある.
個ある.
そのうち![]() を含むものを
を含むものを
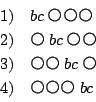
従って![]() を含む相異なるワードは
を含む相異なるワードは
解2
![]() 文字からなる文字列
文字からなる文字列![]() を含まないワードのうち,
を含まないワードのうち,
![]() から始まるものが
から始まるものが![]() 個,
個,
![]() から始まるものが
から始まるものが![]() 個,
個,
![]() から始まるものが
から始まるものが![]() 個とする.
個とする.
![]() 文字からなるワードの左側に次の文字をおくと考えると,
文字からなるワードの左側に次の文字をおくと考えると,