1歩で1段または2段のいずれかで階段を昇るとき,1歩で2段昇ることは連続しないものとする.15段の階段を昇る昇り方は何通りあるか.
方針
解1
2段昇りを![]() 回するとする.1段昇りは
回するとする.1段昇りは![]() 回である.
1段昇りの間に2段昇りを組み込めば,一つの昇り方が決まる.
最初や最後が2段昇りでもよい.よって2段昇りを
回である.
1段昇りの間に2段昇りを組み込めば,一つの昇り方が決まる.
最初や最後が2段昇りでもよい.よって2段昇りを![]() 回する昇り方は
回する昇り方は
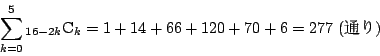
解2
![]() 段を条件を満たして昇る昇り方が
段を条件を満たして昇る昇り方が![]() 通りあるとする.
通りあるとする.
![]() に対して,
それぞれ昇る段数は,
に対して,
それぞれ昇る段数は,
![]() となるので,
となるので,
![]() である.
である.
![]() のとき,
のとき,![]() 段の昇りを最初の昇り方で場合に分ける.
段の昇りを最初の昇り方で場合に分ける.