![]() 枚の100円玉と
枚の100円玉と![]() 枚の500円玉を同時に投げたとき,表の出た100円玉の枚数より表の出た500円玉の枚数の方が多い確率
枚の500円玉を同時に投げたとき,表の出た100円玉の枚数より表の出た500円玉の枚数の方が多い確率![]() を求めよ.
を求めよ.
方針
解1
100円玉が![]() 枚表になったときは,500円玉が
枚表になったときは,500円玉が![]() 枚以上表になればよい.
したがって
枚以上表になればよい.
したがって
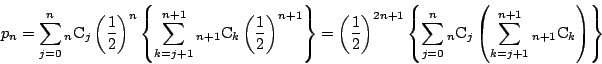
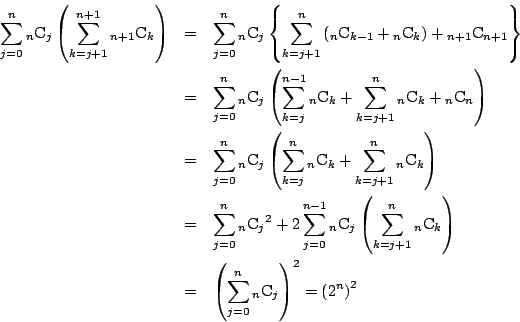
余事象は、100円玉が![]() 枚表になったとき,500円玉で表であるものが
枚表になったとき,500円玉で表であるものが![]() 枚以下になればよい.
したがって
枚以下になればよい.
したがって
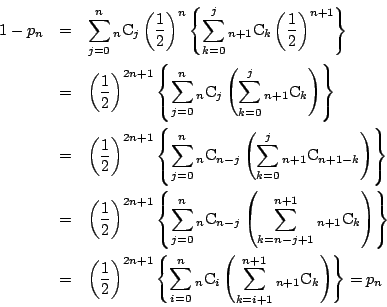
解3
500円玉を一つ固定する.
1回の試行で,この500円玉が表,裏である結果を「表」,「裏」と表す.
また,![]() 枚の100円玉と残る
枚の100円玉と残る![]() 枚の500円玉の表の枚数を
枚の500円玉の表の枚数を![]() と
と![]() とおく.
試行のすべての結果は次の6通りに場合分けされ,それぞれ事象を定める.
とおく.
試行のすべての結果は次の6通りに場合分けされ,それぞれ事象を定める.
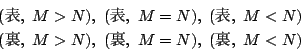
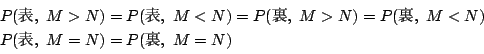
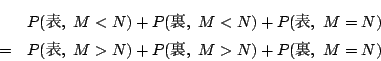
解4
