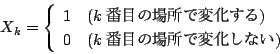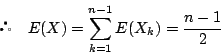次: 確率変数の加法性[91年京大文理系]
上: 確率計算の方法
前: 事象の分解[05京大後期理系]
次: 確率変数の加法性[91年京大文理系]
上: 確率計算の方法
前: 事象の分解[05京大後期理系]
問題
 を3以上の自然数とする.スイッチを入れると等確率で赤色または青色に輝く電球が横一列に
を3以上の自然数とする.スイッチを入れると等確率で赤色または青色に輝く電球が横一列に 個並んでいる.
これらの
個並んでいる.
これらの 個の電球のスイッチを同時に入れたあと,左から電球の色を見ていき,色の変化の回数を調べる.
個の電球のスイッチを同時に入れたあと,左から電球の色を見ていき,色の変化の回数を調べる.
- 赤青…青,赤赤青…青,……のように左端が赤色で色の変化がちようど1回起きる確率を求めよ.
- 色の変化が少なくとも2回起きる確率を求めよ.
- 色の変化がちょうど
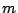 回
回
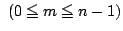 起きる確率を求めよ.
起きる確率を求めよ.
- 色の変化の回数の期待値を求めよ.
方針
3番までは普通の問題である.小問4について,次のように2つの方法がある.
- 1.
- 直接計算.二項係数の性質
を用いる.
- 2.
- 回数を数える確率変数を導入し,確率変数の和の公式
を用いる.
- 色の変化が起こる場所(電球と電球の間と考えればよい)は
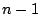 通りある.
1つの場所で色が変化する確率は青赤か赤青なので
通りある.
1つの場所で色が変化する確率は青赤か赤青なので
ゆえに1回だけ色が変化する確率は
左端が赤色の場合と青の場合が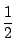 ずつなので,求める確率は
ずつなので,求める確率は
- 1つの場所で色が変化しない確率も
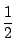 である.
ゆえに
である.
ゆえに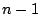 カ所で色が変化しない確率は
カ所で色が変化しない確率は
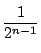 である.
である.
また1回変化する確率は
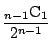 である.
である.
したがって色の変化が少なくとも2回起きる確率は,
- 同様に考え
- 色の変化の回数を
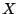 とおく.
とおく.
(4)の別解
確率変数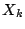 を
を
で定める.
である.また
である.
Aozora Gakuen
![]() を3以上の自然数とする.スイッチを入れると等確率で赤色または青色に輝く電球が横一列に
を3以上の自然数とする.スイッチを入れると等確率で赤色または青色に輝く電球が横一列に![]() 個並んでいる.
これらの
個並んでいる.
これらの![]() 個の電球のスイッチを同時に入れたあと,左から電球の色を見ていき,色の変化の回数を調べる.
個の電球のスイッチを同時に入れたあと,左から電球の色を見ていき,色の変化の回数を調べる.
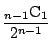 である.
である.
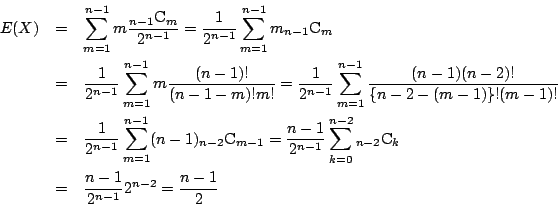
![]() を
を