次: 角の二等分線［09阪大文理］ 上: 平面図形のとらえ方 前: 図形のとらえ方

辺上の点の配置［03京大後期理系］

問題     

正三角形ABCの 辺AB上に点 $\mathrm{P_1}，\mathrm{P_2}$が， 辺BC上に点 $\mathrm{Q_1}，\mathrm{Q_2}$が， 辺CA上に点 $\mathrm{R_1}，\mathrm{R_2}$があり， どの点も頂点には一致していないとする． このとき三角形 $\mathrm{P_1Q_1R_1}$の重心と三角形 $\mathrm{P_2Q_2R_2}$の重心が一致すれば， $\mathrm{P_1P_2}=\mathrm{Q_1Q_2}=\mathrm{R_1R_2}$が成り立つことを示せ．

方針 普通はこれはベクトルの内分点の理論で解く． しかし重心が一致することは何を意味するのか図形的に考えることもできる． この別解は2年生が授業で発表したのだそうだ． そのことを担当の先生に教えられた．

解1

基準点$\mathrm{O}$をとり，$i=1,\ 2$に対して，

$$\begin{eqnarray*} && \overrightarrow{\mathrm{OP}_i}= (1-p_i)\overrightarrow{\mat... ...r_i)\overrightarrow{\mathrm{OC}}+r_i\overrightarrow{\mathrm{OA}} \end{eqnarray*}$$

とおく．重心が一致するので

$$\dfrac{1}{3}\left(\overrightarrow{\mathrm{OP}_1}+\overrighta... ...htarrow{\mathrm{OQ}_2}+ \overrightarrow{\mathrm{OR}_2} \right)$$

これから

$$(-p_1+r_1)\overrightarrow{\mathrm{OA}}+(p_1-q_1)\overrightar... ...rightarrow{\mathrm{OB}} +(q_2-r_2)\overrightarrow{\mathrm{OC}}$$

$\overrightarrow{\mathrm{OC}}=\alpha\overrightarrow{\mathrm{OA}} +\beta\overrightarrow{\mathrm{OB}}$とおく． $\overrightarrow{\mathrm{OA}},\ \overrightarrow{\mathrm{OB}}$は1次独立だから

$$\begin{eqnarray*} &&(-p_1+r_1)+(q_1-r_1)\alpha=(-p_2+r_2)+(q_2-r_2)\alpha\\ &&(p_1-q_1)+(q_1-r_1)\beta=(p_2-q_2)+(q_2-r_2)\beta \end{eqnarray*}$$

辺々加えて移行すると

$$\{(q_1-q_2)-(r_1-r_2)\}(\alpha+\beta-1)=0$$

点Cは直線AB上にないので $\alpha+\beta\ne 1$である．

$$q_1-q_2=r_1-r_2$$

この結果 $p_1-p_2=r_1-r_2$も成り立つ．この値を$k$とおく． よって

$$\begin{eqnarray*} && \overrightarrow{\mathrm{P}_2\mathrm{P}_1}= (p_1-p_2)\overri... ...m{AC}}\\ ∴&&\mathrm{R}_2\mathrm{R}_1=\vert k\vert{\mathrm{AC}} \end{eqnarray*}$$

正三角形なので3辺の長さが等しい．よって

$$\mathrm{P_1P_2}=\mathrm{Q_1Q_2}=\mathrm{R_1R_2}$$

である．

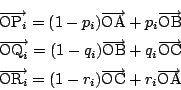
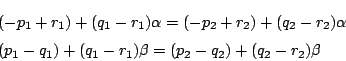
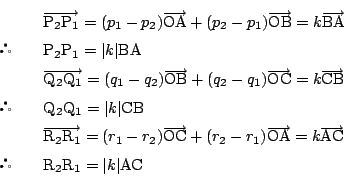
解2

(最初の設定は同じ)

重心の一致から

$$\overrightarrow{\mathrm{OP}_1}+\overrightarrow{\mathrm{OQ}_1... ...\overrightarrow{\mathrm{OQ}_2}+ \overrightarrow{\mathrm{OR}_2}$$

これから

$$\overrightarrow{\mathrm{P}_1\mathrm{P}_2}+\overrightarrow{\m... ...+ \overrightarrow{\mathrm{R}_1\mathrm{R}_2}=\overrightarrow{0}$$

である．基準点$\mathrm{O}$をとり，

$$\overrightarrow{\mathrm{OS}}=\overrightarrow{\mathrm{P}_1\ma... ...htarrow{\mathrm{ST}}=\overrightarrow{\mathrm{Q}_1\mathrm{Q}_2}$$

で二点 $\mathrm{S},\ \mathrm{T}$を定める．このとき

$$\overrightarrow{\mathrm{TO}}=-\left(\overrightarrow{\mathrm{... ...mathrm{Q}_2} \right)=\overrightarrow{\mathrm{R}_1\mathrm{R}_2}$$

となる． 辺の平行性から

$$\bigtriangleup \mathrm{OST}∽\bigtriangleup \mathrm{ABC}$$

である． $\bigtriangleup \mathrm{ABC}$が正三角形なので $\bigtriangleup \mathrm{OST}$も正三角形． つまり $\mathrm{OS}=\mathrm{ST}=\mathrm{TO}$．よって

$$\mathrm{P_1P_2}=\mathrm{Q_1Q_2}=\mathrm{R_1R_2}$$

である．