次: 正四面体［05北大］ 上: 空間図形のとらえ方

共線を示す［66京大］

問題     

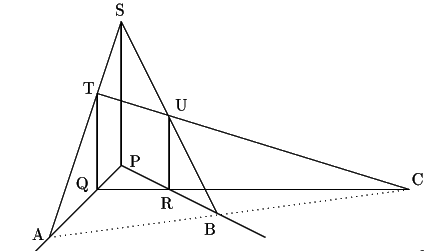
平地に 3 本のテレビ塔がある．ひとりの男がこの平地の異なる 3 地点 A，B，C に立って， その先端を眺めたところ，どの地点でもそのうち2本の先端が重なって見えた． このとき A，B，C は一直線上になければならない．この理由を述べよ．

方針

1.

平面ベクトルを用いて煙突の長さの比から決まってくる条件を書き， 得たい結論もベクトルで書いておいて条件を変形すれば必然的にできる． かならずできる方法である．

2.

メネラウスの定理を使ってみよう．

3.

空間図形としてとらえるとどのようになるか． 空間の3点は一つの平面を定める． 平面と平面の交わりは直線である！

解1

2本の先端が重なって見えたので，3本とも長さが違う．2本の先端が重なって見えたので，3本とも長さが違う．なぜなら，もし同じなら，先端を結ぶ直線が平地と平行となり， 平地から先端を重寝てみることはできない．3本の長さを $l>m>n$ とし， 最長のものから順にテレビ塔をPS，QT，RU とする． このとき

$$\begin{eqnarray*} \overrightarrow{\mathrm{PQ}}&=&\dfrac{l-m}{l}\overrightarrow{\... ...tarrow{\mathrm{QR}}&=&\dfrac{m-n}{m}\overrightarrow{\mathrm{QC}} \end{eqnarray*}$$

 

$$\begin{eqnarray*} \overrightarrow{\mathrm{PC}}&=&\overrightarrow{\mathrm{PQ}}+\o... ...\mathrm{PA}} +\dfrac{m(l-n)}{l(m-n)}\overrightarrow{\mathrm{PB}} \end{eqnarray*}$$

ここで

$$\dfrac{-n(l-m)}{l(m-n)}+\dfrac{m(l-n)}{l(m-n)}=\dfrac{-ln+mn+lm-mn}{l(m-n)}=1$$

ゆえに点 C は直線 AB 上にある．□

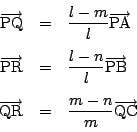
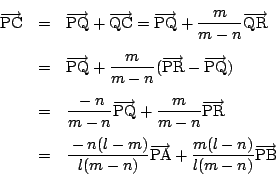
解2

設定は解1と同様とする．

SP,TQは平行でこれで定まる平面上に，S，T，P，Qがあるので，ST上にあるAもこの平面上にある． この結果，Aは直線PQ上にある． P，Q，Rが共線の場合は，A，B，Cともこの直線上にある．

P，Q，Rが共線でなく三角形を作るとする． $\bigtriangleup \mathrm{PQR}$と 辺$\mathrm{PQ}$，$\mathrm{PR}$，$\mathrm{QR}$の延長線上の点 $\mathrm{A},\ \mathrm{B},\ \mathrm{C}$に関してメネラウスの定理を用いる．

$$\dfrac{\mathrm{AQ}}{\mathrm{PA}}\cdot \dfrac{\mathrm{CR}}{\m... ...athrm{RB}} =\dfrac{m}{l}\cdot \dfrac{n}{m}\cdot \dfrac{l}{n}=1$$

よって3点A，B，C同一直線上にある．□

解3

テレビ塔の先端の3点 S，T，U が共線であれば，A，B，Cが一致し， 問題の条件に反する．よって共線ではない．

テレビ塔の先端の3点 S，T，U が定める平面を $\alpha$ とする． 3点A，B，C は$\alpha$上にある．

一方，3点A，B，C は平面上にもある． $\alpha$ と平地の交わりは直線である．

ゆえにA，B，C は この直線上にある．□

吟味
3点S，T，Uが共線となる場合や， P，Q，Rが共線となる場合を退化した場合というと， それぞれの解法には，退化した場合を除かなければならないものがある．
第1の解答は， メネラウスの定理でもできる内容をベクトルで書いたものだ． これは退化した場合を含めての証明になる．
第2の解答は， メネラウスの定理そのものである． P，Q，Rが三角形を作らない場合を先に断る．
第3の解では，3点S，T，Uが共線の場合を先に断る．

第3の方法はずいぶん違うように見える．

実は「射影幾何学」という立場に立てば， 第3の方法も，平面上のメネラウスの定理を 空間図形から理解するというよく知られた， 「同じことの二つの側面」なのだ． 受験問題の解答としては，やはりみごとな解答というべきだろう． これについては『数学対話』の「デザルグの定理」を参照のこと。