

 次: 楕円の接線[87一橋] 上: 平面図形のとらえ方
前: 円の束[91東大後期]
次: 楕円の接線[87一橋] 上: 平面図形のとらえ方
前: 円の束[91東大後期]
問題
平面上の点Oを中心とし半径1の円周上に相異なる3点A,B,Cがある.
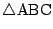 の内接円の半径
の内接円の半径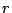 は
は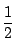 以下であることを示せ.
以下であることを示せ.
方針
- 1.
- 三角形の内角を用いて証明すべき不等式を表してみよう.
三角形の内角の三角比は,和が
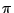 であることを生かして,
さまざまの変形ができる.
であることを生かして,
さまざまの変形ができる.
- 2.
- 3辺の長さをもとに示してみよう.
そのときは内接円の半径
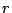 を辺の長さで表すことが第一である.
次に,内接円の半径を辺の長さと関連づけるには,
内心をベクトル表示することが大切である.
内心は頂角の二等分線の交点である.
式変形をいろいろ試みる.
等号成立のときは外心と内心が一致するときであるはずなので,
を辺の長さで表すことが第一である.
次に,内接円の半径を辺の長さと関連づけるには,
内心をベクトル表示することが大切である.
内心は頂角の二等分線の交点である.
式変形をいろいろ試みる.
等号成立のときは外心と内心が一致するときであるはずなので,
 を調べてみる.
を調べてみる.
- 3.
- 外接円,内接円を描き,方べきの定理などを用いて図形的に論証することはできるか.
できる.角と線分の長さを書き込み,何が言えるか考えよう.
解1
各頂点
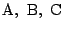 の内角を
の内角を
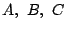 とする.
とする.
である.
正弦定理から3辺の長さは
である.これを用いて,
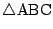 の面積を2通りの方法で求める.
の面積を2通りの方法で求める.
一方,
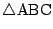 を,内心を頂点とし各辺を1辺とする3つの三角形に分割することにより,
を,内心を頂点とし各辺を1辺とする3つの三角形に分割することにより,
これから
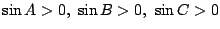 なので,
なので,
を得る.
などが成りたつ.よって
また,
であるから,証明すべき不等式:
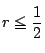 は
は
と同値である.
さらに,
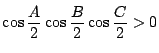 なので,
なので,
と同値である.ところが
より,これは成立する.
等号が成立するのは
のときである.これから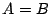 かつ
かつ
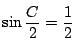 .
.
すなわち
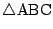 が正三角形のとき
が正三角形のとき
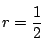 である.□
である.□
解2
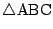 の頂点の対辺の長さを
の頂点の対辺の長さを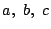 とする.
また内心を
とする.
また内心を とする.
とする.
正弦定理から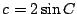 なので
なので
一方内接円の半径が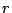 なので
なので
である.
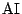 は
は
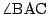 の二等分線なので,
の二等分線なので,
と表せる.同様に
これを始点を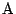 にして書くと
にして書くと
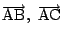 は1次独立なので
は1次独立なので
 を外接円の中心とし,
を外接円の中心とし,
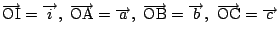 とおく.
とおく.
となる.
次に
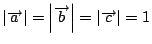 であるから
であるから
などより
である.
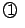 より
より
等号成立は
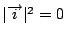 より外心と内心が一致するとき,つまり正三角形のときである.
□
より外心と内心が一致するとき,つまり正三角形のときである.
□
解3
鈍角三角形やと直角三角形では明らかに
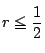 なので,
なので,
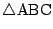 は鋭角三角形とする.
内心を
は鋭角三角形とする.
内心を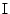 ,外心を
,外心を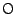 とする.
とする.
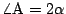 ,
,
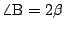 とおく.
とおく.
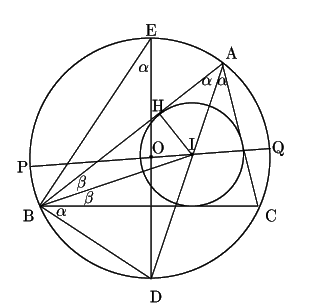 図のように,AIと外接円の交点をD,Dを通る直径をDEとする.
また内心Iから辺ABへの垂線の足をHとする.
さらに内心Iを通る直径をPQとする.
図のように,AIと外接円の交点をD,Dを通る直径をDEとする.
また内心Iから辺ABへの垂線の足をHとする.
さらに内心Iを通る直径をPQとする.
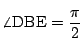 で
で
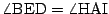 より,
より,
この結果
よって
次に図のように
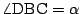 なので
なので
より
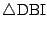 は2等辺三角形.よって
は2等辺三角形.よって
 .
この結果
.
この結果
一方,方べきの定理から
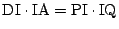 であるので,
であるので,
これから
で等号成立は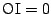 ,
つまり
,
つまり
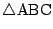 の内心と外心が一致するときで正三角形のときである.□
の内心と外心が一致するときで正三角形のときである.□
吟味
- 1.
- この問題は実にさまざまの解法がある.
この他にも,
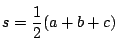 とおいて,
とおいて,
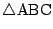 の面積
の面積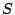 を
を
と3通りに表して示す方法もある.やってみてほしい.
- 2.
- 解法1のなかの不等式
の証明は次のような別解もある.
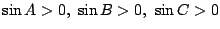 なので相加平均・相乗平均の不等式から
なので相加平均・相乗平均の不等式から
が成り立つ.両辺3乗して4倍すると
したがって
を示せばよい.
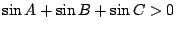 なので,これは
なので,これは
と同値である.これは
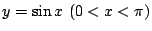 で上に凸であることを用いて示せる.
で上に凸であることを用いて示せる.
3点
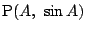 ,
,
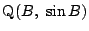 ,
,
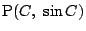 をとるとその重心
をとるとその重心
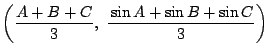 は
は
 の内部にありその結果重心は領域
の内部にありその結果重心は領域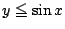 にある.
これから
にある.
これから
となる.
これは 「99年後期理系」と同様である.
- 3.
-
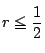 を次のように示すこともできる.
を次のように示すこともできる.
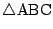 内接円とは,
3つの辺と共有点をもつ円のうち半径が最小の円である.
内接円とは,
3つの辺と共有点をもつ円のうち半径が最小の円である.
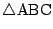 の
3つの辺AB,BC,CA の中点を
の
3つの辺AB,BC,CA の中点を
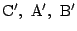 とする.
とする.
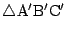 は
は
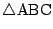 と相似で相似比は
と相似で相似比は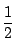 である.
である.
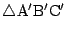 の外接円
の外接円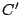 の半径は
の半径は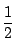 で,
この円は
で,
この円は
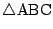 の3辺と共有点
の3辺と共有点
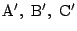 をもっている.
をもっている.
よって
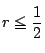 である.
である.
この場合,等号成立するのが正三角形しかないことをいうところで何らかの工夫がいる.


 次: 楕円の接線[出典不明]
上: 平面図形のとらえ方
前: 円の束[91東大後期]
Aozora Gakuen
次: 楕円の接線[出典不明]
上: 平面図形のとらえ方
前: 円の束[91東大後期]
Aozora Gakuen
![]() の内接円の半径
の内接円の半径![]() は
は![]() 以下であることを示せ.
以下であることを示せ.
![]() の内角を
の内角を
![]() とする.
とする.
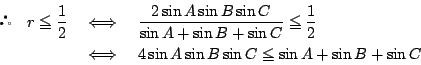
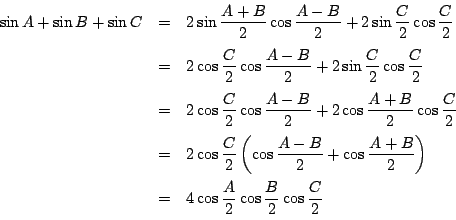
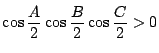 なので,
なので,
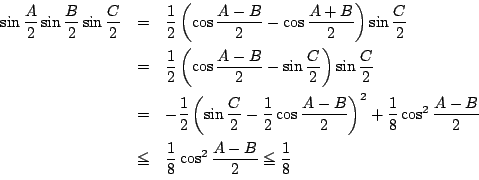
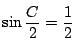 .
.
![]() の頂点の対辺の長さを
の頂点の対辺の長さを![]() とする.
また内心を
とする.
また内心を![]() とする.
とする.
![]() なので
なので
![]() は
は
![]() の二等分線なので,
の二等分線なので,
![]() を外接円の中心とし,
を外接円の中心とし,
![]() とおく.
とおく.
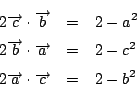
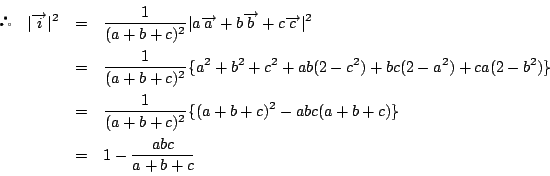
![]() より
より
![]() なので,
なので,
![]() は鋭角三角形とする.
内心を
は鋭角三角形とする.
内心を![]() ,外心を
,外心を![]() とする.
とする.
![]() ,
,
![]() とおく.
とおく.
 図のように,AIと外接円の交点をD,Dを通る直径をDEとする.
また内心Iから辺ABへの垂線の足をHとする.
さらに内心Iを通る直径をPQとする.
図のように,AIと外接円の交点をD,Dを通る直径をDEとする.
また内心Iから辺ABへの垂線の足をHとする.
さらに内心Iを通る直径をPQとする.
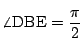 で
で
![]() より,
より,
![]() なので
なので
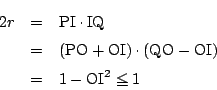
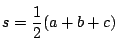 とおいて,
とおいて,
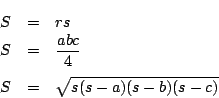
![]() なので相加平均・相乗平均の不等式から
なので相加平均・相乗平均の不等式から
![]() ,
,
![]() ,
,
![]() をとるとその重心
をとるとその重心
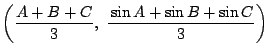 は
は
![]() の内部にありその結果重心は領域
の内部にありその結果重心は領域![]() にある.
これから
にある.
これから
内接円とは, 3つの辺と共有点をもつ円のうち半径が最小の円である.
の 3つの辺AB,BC,CA の中点を
とする.
は
と相似で相似比は
である.
の外接円
の半径は
で, この円は
の3辺と共有点
をもっている.
である.