平面上に3つの円
![]() があって,
があって, ![]() と
と![]() は相異なる2点
は相異なる2点 ![]() ,
, ![]() で交わり,
で交わり, ![]() は
は ![]() および
および ![]() と互いに直交している.ただし,2つの円がたがいに直交しているとは,2つの円に共通点があって,各共通点におけるそれぞれの円に対する接線が共通点で直交しているときをいう.
と互いに直交している.ただし,2つの円がたがいに直交しているとは,2つの円に共通点があって,各共通点におけるそれぞれの円に対する接線が共通点で直交しているときをいう.
方針
ところが(2)を式にかいてやろうとすると,なかなか難しい. (1)の結果を使うと,方べきの定理を使うことができる.
解1
(1)
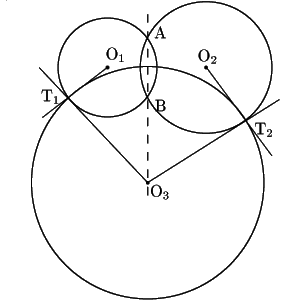 円
円
![]() の中心と半径をそれぞれ
の中心と半径をそれぞれ
![]() ,
,
![]() とする.
また2つの接点を
とする.
また2つの接点を
![]() とする.
三平方の定理より
とする.
三平方の定理より
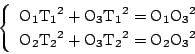
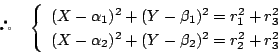
(2)
円 ![]() と円外の点
と円外の点 ![]() および
および ![]() を通る直線
を通る直線 ![]() に関して方べきの定理を用いる.
に関して方べきの定理を用いる.
(1)の解2
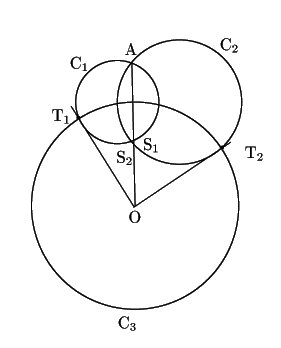 円
円![]() の中心を
の中心を![]() とする.
とする.
![]() から2円
から2円
![]() への接線を
への接線を
![]() とする.
とする.
![]() が
が![]() および
および![]() と互いに直交しているので,接点
と互いに直交しているので,接点
![]() はそれぞれ
円
はそれぞれ
円![]() 上にある.
上にある.
直線![]() が点
が点![]() を通らず,
円
を通らず,
円
![]() とそれぞれ
とそれぞれ
![]() で交わったとする.
で交わったとする.
円
![]() における方べきの定理から
における方べきの定理から
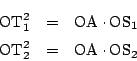
この問題は,一つは2つの円の根軸に関する一般論が背景になっている.これについては『数学対話』−「根軸」を見てほしい.
また2つの解法をつなぐのは,方べきの定理の図形的証明と座標的証明だ.座標で示すのはやや複雑であるが,いちどはやってみておくべきである.