

 次: 三角関数の不等式[05京大後期文系]
上: 関数と方程式・不等式
前: 連立三角方程式[66静岡大]
次: 三角関数の不等式[05京大後期文系]
上: 関数と方程式・不等式
前: 連立三角方程式[66静岡大]
問題
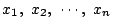 を実数,
を実数, を自然数とする.このとき
を自然数とする.このとき
が成立することを示せ.
方針
-
- 1.
- 数学的帰納法.
- 2.
- 直接の変形.
- 3.
- コーシー・シュワルツの不等式.
- 4.
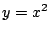 という下に凸な関数を用いる.
という下に凸な関数を用いる.
解1
任意の実数
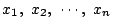 と,自然数
と,自然数 に対し,不等式
に対し,不等式
が成立することを数学的帰納法で示す.
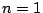 のとき.
のとき.
 は
は
となり,成立.
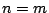 のとき命題が成立するとする.
のとき命題が成立するとする.
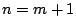 のとき.
のとき.
数学的帰納法の仮定から
なので,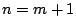 のときも
のときも は成立する.
は成立する.
かつ での等号成立が
での等号成立が
のときであることも示された.
□
解2
直接示す.
和
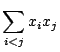 では,どの文字もちょうど
では,どの文字もちょうど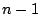 回ずつ現れる.
したがって
回ずつ現れる.
したがって
である.つまり
等号成立は
のとき.
□
解3
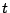 を実数の変数にとり,2次式
を実数の変数にとり,2次式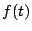 を
を
とおく.
である.任意の実数値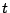 に対して
に対して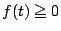 であるから,その判別式
であるから,その判別式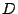 は
は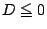 である.
である.
より
が示された.等号成立は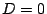 ,つまり
,つまり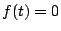 となる実数
となる実数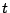 が存在するときである.
よって
が存在するときである.
よって
となる実数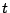 が存在するときである.これは
が存在するときである.これは
となる実数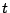 が存在するときである.つまり
等号成立は
が存在するときである.つまり
等号成立は
のとき.
□
解4
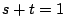 である正の数と,実数
である正の数と,実数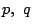 に関して
に関して
実際,
である.ここで等号成立は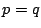 のときである.また
のときである.また
そこで,この不等式の成立と
等号成立が
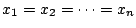 のときであることを,
のときであることを,
 についての数学的帰納法で示す.
についての数学的帰納法で示す.
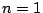 のときは
のときは
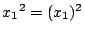 で成立する.
で成立する.
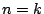 で成立するとする.
で成立するとする.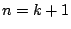 のとき
のとき
等号成立は
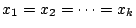 かつ
かつ
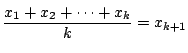 ,つまり
,つまり
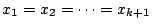 のときである.
よって
のときである.
よって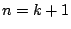 のときも成立し,すべての
のときも成立し,すべての で成立した.
□
で成立した.
□
吟味
この問題の不等式は,コーシー・シュワルツの不等式と,凸関数の不等式の両方の性質をもつ不等式である.それぞれの方向に一般化することができる.



次: 不等式と凸関数[99京大後期理系]
上: 関数と方程式・不等式
前: 連立三角方程式[66静岡大]
Aozora Gakuen
![]() を実数,
を実数,![]() を自然数とする.このとき
を自然数とする.このとき
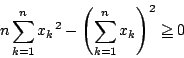
![]() と,自然数
と,自然数![]() に対し,不等式
に対し,不等式
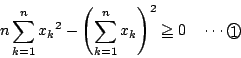
![]() のとき.
のとき.
![]() は
は
![]() のとき命題が成立するとする.
のとき命題が成立するとする.
![]() のとき.
のとき.
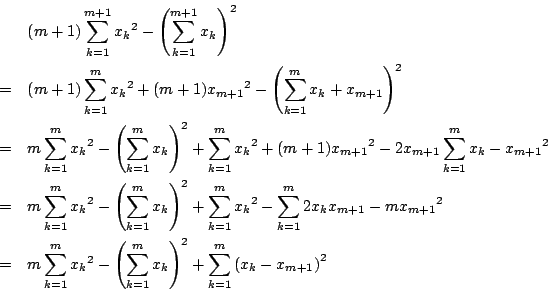
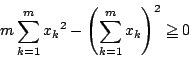
![]() での等号成立が
での等号成立が
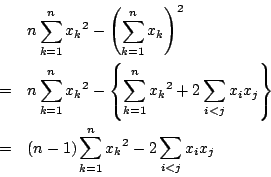
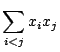 では,どの文字もちょうど
では,どの文字もちょうど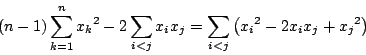
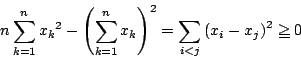
![]() を実数の変数にとり,2次式
を実数の変数にとり,2次式![]() を
を
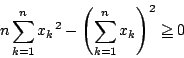
![]() である正の数と,実数
である正の数と,実数![]() に関して
に関して
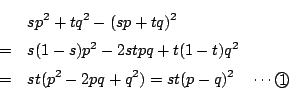
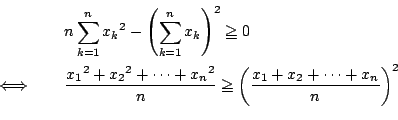
![]() のときは
のときは
![]() で成立する.
で成立する.
![]() で成立するとする.
で成立するとする.![]() のとき
のとき
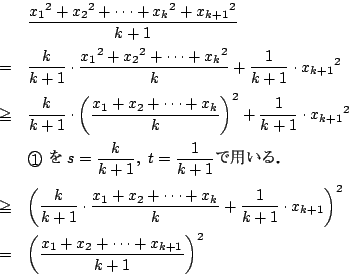
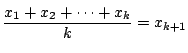 ,つまり
,つまり