正像法では次のように実際の値域の必要条件から考える.
逆像法での別解は次のように変数の存在条件から求める.
![]() のとりうる範囲は
のとりうる範囲は![]() となる実数
となる実数 ![]() が存在する範囲,である.
が存在する範囲,である.
![]() より
より
![]() .
.
第一の方法を「正像法」,第二の方法を「逆像法」と呼ぶことが多い. これを「順手法」「逆手法」という人もいるが,第二の方法が論理的には大切なのに 何か「裏技」のような印象の言葉なので私は使わない. 「正像法と逆像法」はもちろん次のような通過領域で用いることが多い.
問題
![]() 平面上の直線
平面上の直線![]() がある.
がある.![]() が
が ![]() を動くとき, この直線が通過する
を動くとき, この直線が通過する![]() 平面の領域を求めよ.
平面の領域を求めよ.
方針
解1
![]() を固定し,各
を固定し,各 ![]() に対して
に対して![]() がとりうる範囲を
がとりうる範囲を ![]() で表す.
で表す.
その範囲は右辺を ![]() の2次関数と見たときの軸
の2次関数と見たときの軸
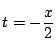 の
位置で場合分けし,最大最小を求めれば定まる.
の
位置で場合分けし,最大最小を求めれば定まる.
右辺の ![]() の2次関数を
の2次関数を ![]() と置く.
と置く.
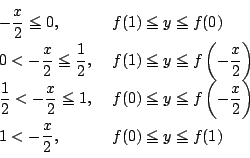
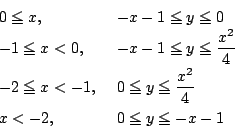
解2
点 ![]() が通過領域にあるということは
が通過領域にあるということは![]() となる
となる ![]() が
が
![]() に存在することと同値である.
に存在することと同値である.
![]() と置く.
と置く.
![]() を
を ![]() の2次方程式
の2次方程式 ![]() の判別式とすれば,
求める条件は次のいずれかがなり立つことである.
の判別式とすれば,
求める条件は次のいずれかがなり立つことである.
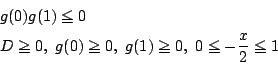
吟味
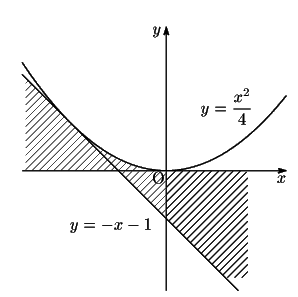
場合分けの仕方が違うがいずれも図示すれば同じものになる.
このように正像法と逆像法は,簡単なときはどちらでも同じことだ.論証としては媒介変数の 存在条件から求める逆像法が論述しやすいが,関数が簡単にならないときは実際に実行するのは 難しくなる.その例が『数学対話』「包絡線」にある. 正像法は考えやすいが,条件が複雜なときに厳密に求めるのが難しいときがある. 双方をよく理解した上で,使い分けることが大切だ.