問題
![]() は
は
![]() ,
,
![]() を満たすものとする.このとき,
を満たすものとする.このとき,
![]() の最大値を求めよ.
の最大値を求めよ.
方針
2変数の関数の最大最小を求めるのは1文字を固定して考える.
まず
![]() とおいて,
とおいて,
![]() の関数として
最大を
の関数として
最大を ![]() の入った形で求め,それから
の入った形で求め,それから ![]() を動かせばよい.
を動かせばよい.
解1
![]() を消去し,
を消去し,![]() を固定して考える.
を固定して考える.
![]() で
で![]() より
より
![]() ,
つまり
,
つまり
![]() ,
この範囲の
,
この範囲の ![]() に対して
に対して
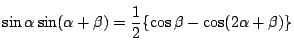 なので
なので
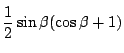 である.
である.
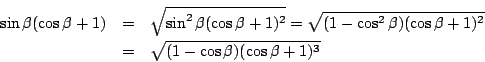
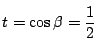 より,
より,
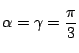 である.
である.
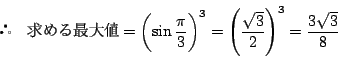 □
□

解2
![]() ,
,
![]() より,この3角を内角とする
三角形が存在する.
より,この3角を内角とする
三角形が存在する.
![]() の最大値を求めるためには,
三角形の外接円の半径を1としてよい.三つの角の対辺の長さを
の最大値を求めるためには,
三角形の外接円の半径を1としてよい.三つの角の対辺の長さを ![]() とすると
正弦定理より
とすると
正弦定理より
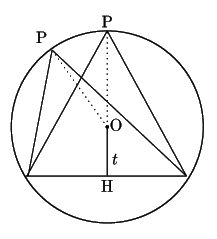 したがって求める最大値は,半径1の円に内接する三角形の面積の最大値の
したがって求める最大値は,半径1の円に内接する三角形の面積の最大値の
底辺の長さが![]() で高さが
で高さが ![]() なので面積は
なので面積は
このとき三角形は正三角形である.□
解3
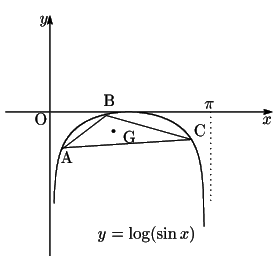
![]() に対し
に対し
したがって,3点
![]() ,
,
![]() ,
,
![]() でつくる
でつくる
![]() は領域
は領域
![]() にある.
にある.
したがって ![]() も領域
も領域 ![]() にある.つまり
にある.つまり
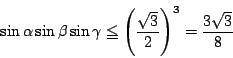
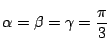 の
とき最大値は
の
とき最大値は

吟味
さてこの三つの解法を比較検討してみよう.
2変数の関数の最大値は.まず1変数を固定し順次最大値を定めていけ,
という考え方は一般的だ.
こういう場面でそれが思い起こせるようにしたい.
第1の解法で
![]() の関数として考えるということがはっきりしていれば,
数学III範囲になるが
の関数として考えるということがはっきりしていれば,
数学III範囲になるが
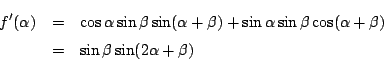
それに対して第2の解法は三角形の面積に還元するうまい方法だ.
しかしこれを ![]() 個の変数の場合に一般化することは難しい.
第3の方法は,
個の変数の場合に一般化することは難しい.
第3の方法は,![]() 個の変数の場合に一般化できる.
『数学対話』「凸多角形と凸関数」にある.
個の変数の場合に一般化できる.
『数学対話』「凸多角形と凸関数」にある.
![]() 個の
個の
![]() はすべて正で
はすべて正で
![]() のとき
のとき
これを解2の方法でやるのは難しい.解1の方法なら,順次最大になる位置を決めていけば不可能ではないが,複雜になる.