

 次: 関数等式[98阪大]
上: 別解研究
前: 不等式と凸関数[99京大後期理系]
次: 関数等式[98阪大]
上: 別解研究
前: 不等式と凸関数[99京大後期理系]
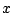 の整式はさまざまの見方をすることができる.
基本的には次の二つの面からとらえることができる.
の整式はさまざまの見方をすることができる.
基本的には次の二つの面からとらえることができる.
- まず多項式である.つまり
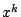 と数係数の積
と数係数の積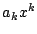 の和
の和
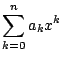 である.
である.
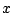 の関数である,しかも実数全体で定義される.
また必要なだけ微分することも積分することもできる.
の関数である,しかも実数全体で定義される.
また必要なだけ微分することも積分することもできる.
従ってまた,恒等式の論証も,多項式としての一致の方から見る係数比較法と,関数の値から見る代入法がある.そしてこれが恒等式の理論によって同値になるのだった.
Aozora Gakuen
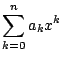 である.
である.
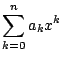 である.
である.