

 次: 関数値の符号[01慶応理工]
上: 整式と見るか関数と見るか
前: 整式と見るか関数と見るか
次: 関数値の符号[01慶応理工]
上: 整式と見るか関数と見るか
前: 整式と見るか関数と見るか
問題
 を1以上の整数とする.
を1以上の整数とする.  次の整式
次の整式
とその導関数 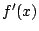 の間に
の間に
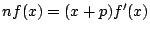 という関係があるとする.ただし,
という関係があるとする.ただし, 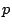 は定数である.このとき,
は定数である.このとき,
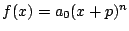 であることを示せ.
であることを示せ.
方針
-
- 1.
 次整式を
次整式を 回微分すると定数になる.
微分によって関数等式がどのように変わるか,
両辺微分して整理する.
回微分すると定数になる.
微分によって関数等式がどのように変わるか,
両辺微分して整理する.
- 2.
- 関数等式から係数の関係式を導く.
一方,
結論からさかのぼると
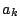 がどのようになってほしいかわかるので,
数学的帰納法で示す.
がどのようになってほしいかわかるので,
数学的帰納法で示す.
- 3.
- 関数等式は微分方程式そのものである.
これを解くにはいちど積分すればよい.
解1
関数等式
の両辺を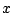 で微分する.
で微分する.
よって,
同様に,
よって,1からnをすべてかけあわせると
ここで,
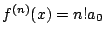 なので
なので
解2
であるから,
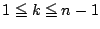 のとき,
のとき, 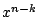 の係数は,
の係数は,
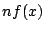 と比較して,
と比較して,
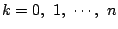 について
について
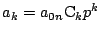 となることを
となることを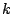 についての数学的帰納法で示す.k=0 のときはそのまま成立する.
についての数学的帰納法で示す.k=0 のときはそのまま成立する.
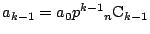 と仮定すると, 上式より,
と仮定すると, 上式より,
また,
よってすべての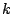 で
で
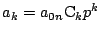 となる.
となる.
解3
より
これから
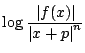 が定数となる.
が定数となる.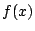 は整式なので
は整式なので
となる定数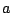 がある.
がある.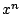 の係数を比較して
の係数を比較して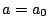 .
.
吟味
-
- 1.
- 条件をどのように使ったかをおさえておこう.
関数等式を微分し整理するところでは,
 回微分可能であることのみ整式であることを使う.
回微分可能であることのみ整式であることを使う.
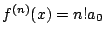 は最高次の係数が
は最高次の係数が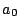 の整式であることを使う.
の整式であることを使う.
- 2.
- これは
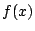 が整式であることを最初から使っている.
が整式であることを最初から使っている.
- 3.
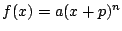 と表されるところまでは,
整式であることは使っていない.
初期条件は,整式であることを前提としている.
と表されるところまでは,
整式であることは使っていない.
初期条件は,整式であることを前提としている.
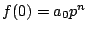 のように与えられれば,整式であることは使わない.
のように与えられれば,整式であることは使わない.



次: 関数値の符号[01慶応理工]
上: 整式と見るか関数と見るか
前: 整式と見るか関数と見るか
Aozora Gakuen
![]() を1以上の整数とする.
を1以上の整数とする. ![]() 次の整式
次の整式
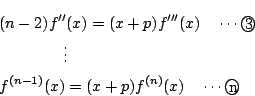
![]() について
について
![]() となることを
となることを![]() についての数学的帰納法で示す.k=0 のときはそのまま成立する.
についての数学的帰納法で示す.k=0 のときはそのまま成立する.
![]() と仮定すると, 上式より,
と仮定すると, 上式より,
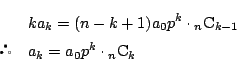
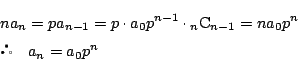
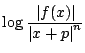 が定数となる.
が定数となる.