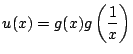 で定義する.
で定義する.
実数![]() に対し
に対し
![]() を考え,
を考え,
![]() を
を
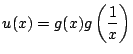 で定義する.
で定義する.
 の整式
の整式
方針
解1
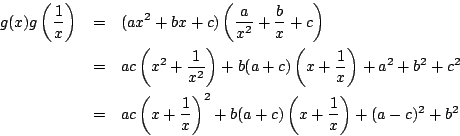
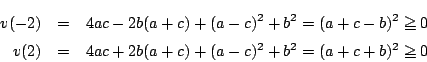
![]() ,または
,または![]() で
で
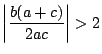 なら,
なら,
![]() で
で ![]() .
.
![]() でかつ
でかつ
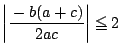 のときは,この条件の下で,
のときは,この条件の下で,
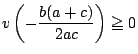 を示せばよい.
を示せばよい.
軸の条件は
![]() となるので
となるので
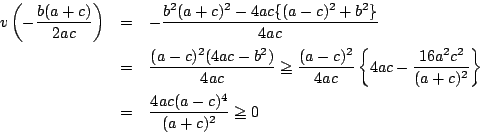
解2
したがってこれは基本対称式 ![]() と
と ![]() の整式である.
の整式である.
![]() と
と ![]() で表したものの
で表したものの ![]() に
に ![]() を代入する.
を代入する.
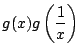 は
は
![]() と
と
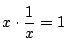 の整式となる.
つまり
の整式となる.
つまり
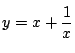 の整式として表せる.
の整式として表せる.
さらに解と係数の関係から
![]() である.
である.
したがって
![]() の範囲のすべての
の範囲のすべての
![]() に対して
に対して ![]() であることが示された.□
であることが示された.□
吟味
第1の解法の(2)は次のようにもできる.
![]() を
を ![]() で整理すると
で整理すると
これは「より個別性を用いたうまい方法」には違いないし,見つければおもしろいが, なかなか気づくとはかぎらない.
さて,より一般的な方法はないか.考えるヒントは
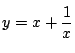 と置いたとき,
と置いたとき,
![]() になるような
になるような ![]() はどんなものかということだ.
はどんなものかということだ.
![]() は2解の積が1の重解か虚数解である.
虚数解の場合2解は
は2解の積が1の重解か虚数解である.
虚数解の場合2解は![]() と
と
![]() とおけ,積が1のなで
とおけ,積が1のなで
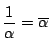 だ.
それが判れば,
だ.
それが判れば,
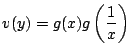 だから,
だから, ![]() の問題を
の問題を
![]() の問題に還元できる.
の問題に還元できる.