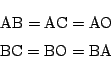例えば
![]() があり,
角の対辺の長さが
があり,
角の対辺の長さが ![]() であるとする.
各辺の長さと角の大きさの間に余弦定理
が成り立つことを証明しようとする.
まず,一つの
であるとする.
各辺の長さと角の大きさの間に余弦定理
が成り立つことを証明しようとする.
まず,一つの![]() について
について
![]() が成り立つことが示せたとする.
すると,他の
が成り立つことが示せたとする.
すると,他の
![]() なども必然的に成り立つ.
なども必然的に成り立つ.
なぜだろうか.
証明の過程ですべての文字について
![]() の置き換えをすれば,それに対応して対辺の長さも
の置き換えをすれば,それに対応して対辺の長さも
![]() に置き換わる.
したがって,
に置き換わる.
したがって,
![]() を示したのとまったく同じ論証の過程を経て
を示したのとまったく同じ論証の過程を経て
![]() が示される.
が示される.
いくつかの文字を含む条件から ある結論を引き出したとする. すると,文字を規則正しく置きかえた結論は 「同様に示される」. 「同様に示される」ことを活用して証明を簡略化できる. これも文字という考え方のもつ大きな力である. この考え方はすでに例題(2.1)の 解答3において用いている.
この論述でも三文字を,および同様に得られる2式
,
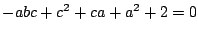
例題 2.4 [03年京大]
四面体OABCは次の2つの条件
(i)
![]()
(ii) 4つの面の面積がすべて等しい
考え方
どの文字についても対称性がある.
つまり,どの頂点に関しても同じ条件である.
このような場合一つの頂点![]() を始点にとって示せたなら
同じ論証はくりかえさなくても,文字を置きかえて得られる結論は,
「同様に」とすることで,くりかえさなくてもよい.
を始点にとって示せたなら
同じ論証はくりかえさなくても,文字を置きかえて得られる結論は,
「同様に」とすることで,くりかえさなくてもよい.
解答
![]() ,
,
![]() ,
,
![]() とおくと, 条件(i)より
とおくと, 条件(i)より