| (2.6) |
![]() の2次方程式(2.6)で,
定数
の2次方程式(2.6)で,
定数![]() が
が ![]() の範囲で変化するとき,
解はどのような範囲にあるか.
の範囲で変化するとき,
解はどのような範囲にあるか.
解答1
(2.6)は ![]() と変形される.
これから二つのグラフ
と変形される.
これから二つのグラフ
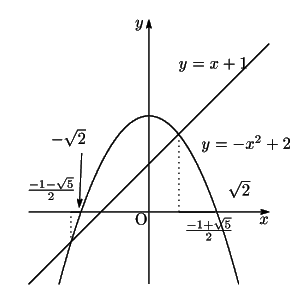 の交点がどのように変化するかを考える.
第2式の直線はつねに
の交点がどのように変化するかを考える.
第2式の直線はつねに
考え方2
しかしさらに考えて見よう.
![]() が求める範囲にあるということは,
が求める範囲にあるということは,
![]() で(2.6)を満たす
で(2.6)を満たす ![]() がとれるということだ.
つまり
がとれるということだ.
つまり![]() の
の ![]() が存在するような範囲として
が存在するような範囲として
![]() の範囲が定まる.
(2.6)は
の範囲が定まる.
(2.6)は ![]() の1次方程式で
の1次方程式で![]() が定数とも考えられる.
このように見れば,
が定数とも考えられる.
このように見れば,
![]() の1次方程式(2.6)が
の1次方程式(2.6)が![]() に解をもつような定数
に解をもつような定数![]() の範囲として,求まることになる.
の範囲として,求まることになる.
解答2
![]() や
や ![]() を変数や未知数,
を変数や未知数,
![]() や
や ![]() を定数と見るのは習慣に過ぎない.
要は二つの文字
を定数と見るのは習慣に過ぎない.
要は二つの文字 ![]() と
と ![]() の間に(2.6)の関係が成り立っている,
ということだけがある.
いずれを変数とし,いずれを定数とするかは固定されていない.
いくつかの文字の混じった式では,
どの文字を固定してどの文字を動かすのかよく考えたい.
また,小問の(1)では定数であったものを(2)では動かすということもよくある.
の間に(2.6)の関係が成り立っている,
ということだけがある.
いずれを変数とし,いずれを定数とするかは固定されていない.
いくつかの文字の混じった式では,
どの文字を固定してどの文字を動かすのかよく考えたい.
また,小問の(1)では定数であったものを(2)では動かすということもよくある.