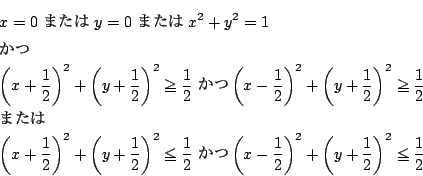-
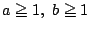 のとき,
次の不等式が成立することを示せ.
のとき,
次の不等式が成立することを示せ.
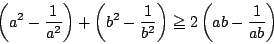
-
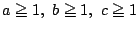 のとき,
次の不等式が成立することを示せ.
のとき,
次の不等式が成立することを示せ.
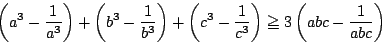
例題 2.6 [07早稲田・教育]
考え方 (1)は 結論の同値変形の一種であるが, 示したい不等式を移項し,左辺−右辺を変形する. 移項したり同類項をまとめたりすることはもっとも基本的な同値変形である. (2)はいろんな方法がある.左辺から右辺を引いた式を,正の部分と負の部分でまとめると,それぞれ因数分解できることに気づきたい.あるいは,3個の場合はできなくても4個ならできることに気づけばそこから道はひらける.
解答
(1)
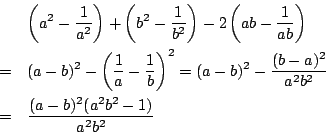
(2) 因数分解と式変形
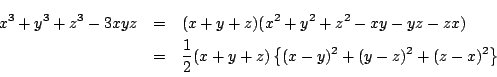
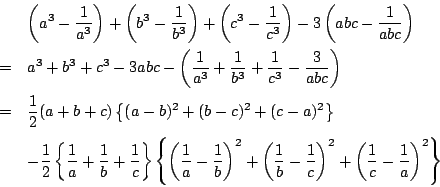
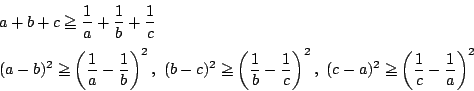
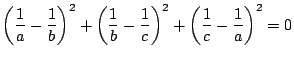 であるから,
これは等号成立の十分条件でもある.
□
であるから,
これは等号成立の十分条件でもある.
□
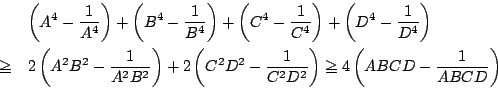
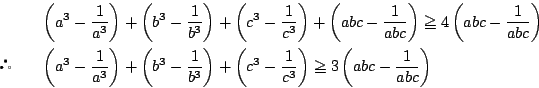
次のような問題でも, 条件と同値な等式をまず立て, それを同値変形することで 点の満たすべき必要十分条件として点の軌跡が求まる.
例題 2.7 [08東大前期文科]
座標平面上の3点
![]() ,
,
![]() ,
,
![]() に対し
に対し
考え方 いろいろと図形的にやりたいのだが,なかなか難しい. あるいは場合分けが必要だ. そこで角の相等という条件を余弦の相等に置きかえ, さらにそれをベクトルで表してその条件と同値な等式を作ろう. それができればその同値変形を行うのだ.
解答
角を![]() 以上
以上![]() 未満にとることにより,条件
未満にとることにより,条件
![]() は,条件
は,条件
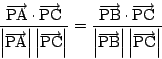
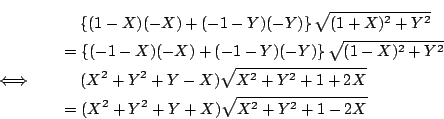
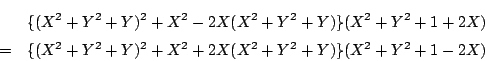
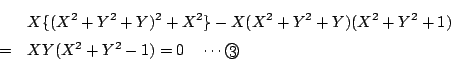
 条件
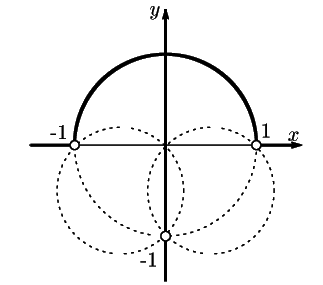
条件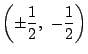 で原点を通る2つの円の共通の外部か共通の内部(と周)である.
よって求める軌跡は
で原点を通る2つの円の共通の外部か共通の内部(と周)である.
よって求める軌跡は