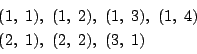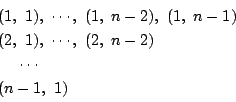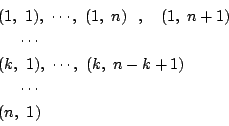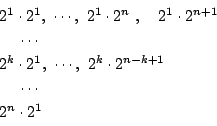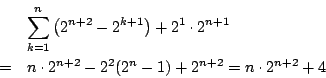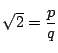 となるものが存在することである.定義からはじめて
となるものが存在することである.定義からはじめて
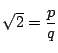 という「式」ができた.これが出発点である.
という「式」ができた.これが出発点である.
第1は,学校で習ったはずの言葉の正確な意味を押さえる,ということである.
例えば,「![]() が無理数であることを示せ」という問題がある.まず「無理数とは何か」がわからなければ解きようがない.「無理数とは有理数でない実数」のことだ.だから,「
が無理数であることを示せ」という問題がある.まず「無理数とは何か」がわからなければ解きようがない.「無理数とは有理数でない実数」のことだ.だから,「![]() が無理数であることを示せ」ということは「
が無理数であることを示せ」ということは「![]() が有理数でないことを示せ」ということだとわかる.これなら証明は背理法でするのが自然だ.
が有理数でないことを示せ」ということだとわかる.これなら証明は背理法でするのが自然だ.![]() が有理数であると仮定する.そこで次は有理数とは何か.「有理数とは分数で表される数」だ.分数は必ず既約分数に出来るから「
が有理数であると仮定する.そこで次は有理数とは何か.「有理数とは分数で表される数」だ.分数は必ず既約分数に出来るから「![]() が有理数である」ということは,互いに素な整数
が有理数である」ということは,互いに素な整数 ![]() と
と ![]() で
で
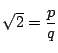 となるものが存在することである.定義からはじめて
となるものが存在することである.定義からはじめて
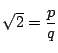 という「式」ができた.これが出発点である.
という「式」ができた.これが出発点である.
また,「自然数 ![]() に対して
に対して![]() と
と ![]() はつねに互いに素であることを示せ.」は
「互いに素」という言葉の意味,つまり定義がわからなければ,どうしようもない.
「1以外に公約数がない」が定義だ.ということは,「最大公約数が1」であることを示せばよい.
そこで
はつねに互いに素であることを示せ.」は
「互いに素」という言葉の意味,つまり定義がわからなければ,どうしようもない.
「1以外に公約数がない」が定義だ.ということは,「最大公約数が1」であることを示せばよい.
そこで![]() と
と ![]() の最大公約数を
の最大公約数を ![]() とし,
とし,![]() と
と ![]() とおく.
とおく.
第2は,出題者が定めた記号の意味を, 自分がわかっている言葉で言い換える,ということである.
「負でない整数![]() の10進法で表した下2桁を
の10進法で表した下2桁を![]() とする」というのが京大文系問題にあった.
出題者がこの記号を使って
とする」というのが京大文系問題にあった.
出題者がこの記号を使って![]() と用いたとしよう.このとき
と用いたとしよう.このとき
また「実数![]() に対して
に対して![]() を超えない最大の整数を
を超えない最大の整数を![]() 」と表す.これはガウス記号といわれ,よく使われる記号だが,日本語で定義された
」と表す.これはガウス記号といわれ,よく使われる記号だが,日本語で定義された![]() の定義に立ちかえれば,
の定義に立ちかえれば,![]() は
は
このように定義に立ちかえることは,数学の問題を解く前提であり,逆にここをはっきりさせることで,問題解決の糸口をつかむことができる.
例題 2.10 [07慶應経済]
![]() を自然数全体の集合とする.集合
を自然数全体の集合とする.集合![]() を
を
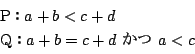
考え方
出題者の定めた新しい記号を定義にしたがってつかみ直し,
既知の記号で表し直せばよい.
また,これは次節の「関係の図示」の方法であるのだが,
![]() を図示しながらつかむとよい.
そこまですると条件を満たす格子点の個数を求める問題だ.
を図示しながらつかむとよい.
そこまですると条件を満たす格子点の個数を求める問題だ.
解答
 (1)
(1)
![]() は
は
![]() または
または![]() の
いずれかを満たす
の
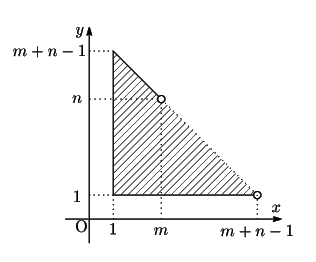
いずれかを満たす![]() の要素からなる.図の斜線および実線上の格子点である.したがって
の要素からなる.図の斜線および実線上の格子点である.したがって![]() の要素は
の要素は