

 次: 数列の図示
上: 関係の図示
前: 関係の図示
次: 数列の図示
上: 関係の図示
前: 関係の図示
関数のグラフとは何か.
関数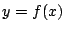 のグラフとは
のグラフとは 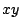 平面上に点の集合
平面上に点の集合
のことだ.これは普通は何らかの曲線になる.
この曲線の形によって,関数の性質が浮かびあがる.
つながっているか切れているか.なめらかか折れ曲がっているか.
右上がりか右下がりか.上に凸か下に凸か.等々.
また,二つの関数のグラフから,
それらの関数相互の関係もいろいろ読みとれるのだった.
これが基本である.
次の例題のように,図を描いて考える典型は,
変域や関数の値域を図示することで問題に見通しをつけることである.
例題 2.11
[98産能大]
解答
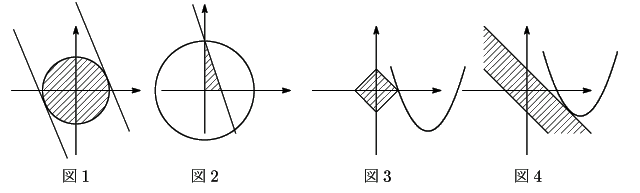
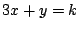 とおく.
とおく.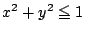 の点に対して
の点に対して 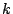 のとりうる値の範囲は,
領域
のとりうる値の範囲は,
領域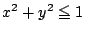 と直線
と直線 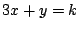 が共有点を持つ範囲として,定まる.
が共有点を持つ範囲として,定まる.
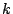 の最大値,最小値は直線
の最大値,最小値は直線 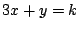 が円
が円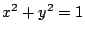 と接するときである.
と接するときである.
最大値は 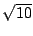 である .
である .
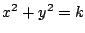 とおくとこれは半径
とおくとこれは半径 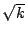 の円.
条件の領域と共有点があるなかで半径最大になるのは,
の円.
条件の領域と共有点があるなかで半径最大になるのは,
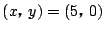 のとき.
最大値
のとき.
最大値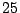 である.
である.
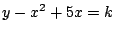 とおくと
とおくと
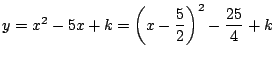 .
軸の位置から図3のときが
.
軸の位置から図3のときが 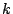 最大.つまり
最大.つまり
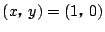 のとき.
最大値は
のとき.
最大値は
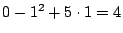 である.
である.
- 同じく図4のように
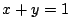 と接するとき.
と接するとき.
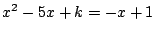 が重解を持つときなので,
が重解を持つときなので, 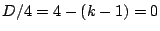 より最大値は
より最大値は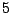 である.
□
である.
□
文字定数を含む方程式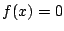 が一定の範囲に解をもつような定数の範囲を求めるとき,これを次のように関数のグラフの共有点で考えると簡明である.
が一定の範囲に解をもつような定数の範囲を求めるとき,これを次のように関数のグラフの共有点で考えると簡明である.
もとの方程式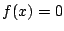 を,
文字定数を含まない部分を左辺に,文字定数を含む部分を右辺に分け,
を,
文字定数を含まない部分を左辺に,文字定数を含む部分を右辺に分け,
とする.
方程式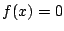 の実数解は,二つの曲線
の実数解は,二つの曲線
のグラフの共有点の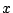 座標である.
座標である.
一般に右辺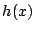 は次数が低くなり(1次か定数の場合が多い)簡単である.
それに対して
は次数が低くなり(1次か定数の場合が多い)簡単である.
それに対して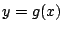 の方は文字定数を含まない固定された関数である.
の方は文字定数を含まない固定された関数である.
例題 2.12
[96関西大]
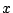 の方程式
の方程式
の異なる解の個数が2つであるために
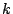
のみたすべき条件を求めよ.
解答
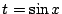 とおく.
とおく.
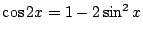 なので
なので
ここで
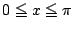 であるから
であるから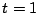 に対して
に対して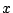 は一つ定まり,
は一つ定まり,
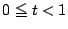 に対して
に対して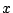 は2つ定まる.したがって
は2つ定まる.したがって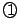 を満たす
を満たす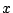 が2つあることは,
が2つあることは,
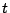 の2次方程式
の2次方程式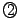 が
が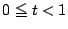 にただ一つの解をもつことと同値である.
にただ一つの解をもつことと同値である.
このことに注意して,
の交点の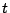 座標がが
座標がが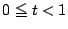 にただ一つあるような
にただ一つあるような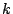 の範囲を求めればよい.
直線
の範囲を求めればよい.
直線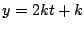 は
は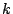 によらずつねに
によらずつねに
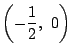 を通る.
を通る.
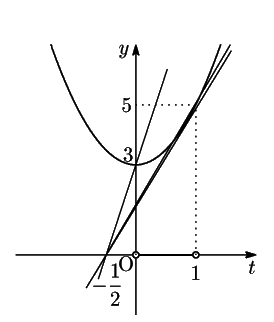 直線
直線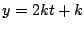 が
が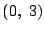 ,
,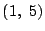 を通るとき,
を通るとき,
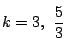 である.
また直線
である.
また直線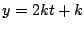 が放物線
が放物線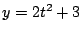 と接するときの
と接するときの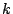 を求める.
を求める.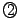 の判別式が
0となる
の判別式が
0となる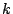 のうち,正のものである.
のうち,正のものである.
より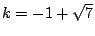 である.
である.
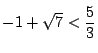 なので,
交点の
なので,
交点の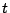 座標がが
座標がが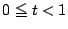 にただ一つあるような
にただ一つあるような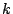 の範囲は
グラフから
の範囲は
グラフから


 次: 数列の図示
上: 関係の図示
前: 関係の図示
Aozora Gakuen
次: 数列の図示
上: 関係の図示
前: 関係の図示
Aozora Gakuen
![]() を実数とするとき,次の問に答えよ.
を実数とするとき,次の問に答えよ.

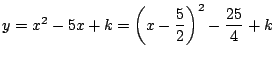 .
軸の位置から図3のときが
.
軸の位置から図3のときが ![]() を,
文字定数を含まない部分を左辺に,文字定数を含む部分を右辺に分け,
を,
文字定数を含まない部分を左辺に,文字定数を含む部分を右辺に分け,
![]() は次数が低くなり(1次か定数の場合が多い)簡単である.
それに対して
は次数が低くなり(1次か定数の場合が多い)簡単である.
それに対して![]() の方は文字定数を含まない固定された関数である.
の方は文字定数を含まない固定された関数である.
![]() の方程式
の方程式
![]() とおく.
とおく.
![]() なので
なので
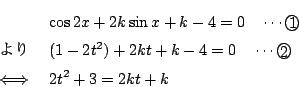
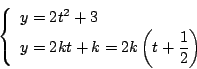
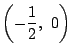 を通る.
を通る.
 直線
直線![]() が
が![]() ,
,![]() を通るとき,
を通るとき,
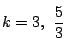 である.
また直線
である.
また直線![]() が放物線
が放物線![]() と接するときの
と接するときの![]() を求める.
を求める.![]() の判別式が
0となる
の判別式が
0となる![]() のうち,正のものである.
のうち,正のものである.
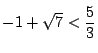 なので,
交点の
なので,
交点の