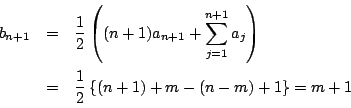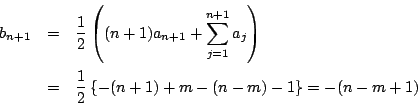次: 一般化して考える
上: 個別と一般
前: 例による型認識
次: 一般化して考える
上: 個別と一般
前: 例による型認識
例から考え,推測したことを証明する典型は,
漸化式と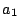 が与えられたときに,
が与えられたときに,
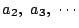 の値を実際に求めて,
それから一般項
の値を実際に求めて,
それから一般項 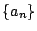 を推測し,
それを数学的帰納法で示すのと同じだ.
「数学的帰納法」
は自然数に関する性質についての命題を
自然数の性質を根拠に示す
間接証明の一つである.
直接証明が難しいときに用いる決定的な方法である.
を推測し,
それを数学的帰納法で示すのと同じだ.
「数学的帰納法」
は自然数に関する性質についての命題を
自然数の性質を根拠に示す
間接証明の一つである.
直接証明が難しいときに用いる決定的な方法である.
そして,「推測してから間接に証明する」というのは
何も自然数に関することにかぎらない一般的な考え方である.
そこで,直前の例題2.16である.
1と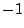 のいろいろな数列を作り結論が推測できたとする.
これを数学的帰納法で示してみよう.
のいろいろな数列を作り結論が推測できたとする.
これを数学的帰納法で示してみよう.
解2
推測の結論2.7が成立することを,
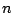 についての数学的帰納法で示す.
についての数学的帰納法で示す.
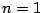 のとき.
のとき.
であるから,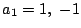 に応じて
に応じて
となり2.7は成立する.
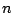 のとき成立するとする.
のとき成立するとする.
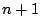 のときにも成立することを示す.
のときにも成立することを示す.
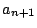 を新たに加える.
を新たに加える.
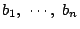 は
は
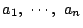 で決まる.
で決まる.
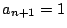 のとき.1が
のとき.1が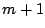 個,
個,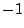 が
が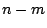 個である.
したがって
個である.
したがって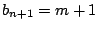 を示せばよい.ところが
を示せばよい.ところが
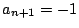 のとき.1が
のとき.1が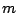 個,
個,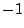 が
が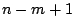 個である.
したがって
個である.
したがって
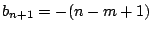 を示せばよい.ところが
を示せばよい.ところが
よって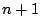 のときにも成立し,2.7は成立する.
□
のときにも成立し,2.7は成立する.
□
Aozora Gakuen
![]() のいろいろな数列を作り結論が推測できたとする.
これを数学的帰納法で示してみよう.
のいろいろな数列を作り結論が推測できたとする.
これを数学的帰納法で示してみよう.
![]() についての数学的帰納法で示す.
についての数学的帰納法で示す.
![]() のとき.
のとき.
![]() のとき成立するとする.
のとき成立するとする.
![]() のときにも成立することを示す.
のときにも成立することを示す.
![]() を新たに加える.
を新たに加える.
![]() は
は
![]() で決まる.
で決まる.
![]() のとき.1が
のとき.1が![]() 個,
個,![]() が
が![]() 個である.
したがって
個である.
したがって![]() を示せばよい.ところが
を示せばよい.ところが