小問で最初に具体的な数で問が立てられ,
次に一般化して![]() の場合を問う,というのはよくあることだが,
そのときにいきなり
の場合を問う,というのはよくあることだが,
そのときにいきなり![]() の場合を考えた方が分かりやすいことがある.
また,そこまでいかなくても,小問の具体的な数の場合を考えるにあたって,
一般化した
の場合を考えた方が分かりやすいことがある.
また,そこまでいかなくても,小問の具体的な数の場合を考えるにあたって,
一般化した![]() の場合に考えやすい方法を探す,
ということも大切なことである.
小問(1)はいろんな方法で解けるだろうが,
次の(2)で一般化を問われたときに通用する方法を(1)で考えなければならない.
の場合に考えやすい方法を探す,
ということも大切なことである.
小問(1)はいろんな方法で解けるだろうが,
次の(2)で一般化を問われたときに通用する方法を(1)で考えなければならない.
このように, 例で考え一般化するというのは,入試問題では, はじめの小問で具体的な例を考えさせるという形でつねに出される. このような場合に大切なことは, 後の小問で一般的な場合に証明する ことに備えて「できるだけ一般的に証明する」ということだ. どのような点に注意して一般化を考えるのか.
そのためには,とにかく何とか解けたときに,一般化を試みておくことだ.問題を一般化して見る.変数の個数を ![]() にする等だ.あるいは条件の一部をはずしてみる.一般化しても成立しそうだと見当をつけたら一般的な場合にも通用する方法を考える.問題が解けてもそれに満足せずこの辺りを考えておく.それは必ず他の場面で生きてくる.一つの問題について,このようないろんな側面から考えたい.違う問題を2題解くより,ひとつの問題を2通りの方法で解く方が,力がつく.なぜならそのことによって,他の関連した問題が一気に解けるようになるからだ.そういう勉強をしてもらいたい.
にする等だ.あるいは条件の一部をはずしてみる.一般化しても成立しそうだと見当をつけたら一般的な場合にも通用する方法を考える.問題が解けてもそれに満足せずこの辺りを考えておく.それは必ず他の場面で生きてくる.一つの問題について,このようないろんな側面から考えたい.違う問題を2題解くより,ひとつの問題を2通りの方法で解く方が,力がつく.なぜならそのことによって,他の関連した問題が一気に解けるようになるからだ.そういう勉強をしてもらいたい.
本質を見抜いた一般化は,証明を簡明にする.しかし,過度な一般化,機械的な一般化は多くの場合証明が出来ないことが多い.それでも一般的に考えようとすることで問題を大きな枠組のなかで考えることができる.そのうえで個別に解く.こうして個別と一般を行き来することが大切なのだ.
まず次の問題を普通に解こう.
例題 2.17 [01慶応理工]
実数![]() に対し
に対し
![]() を考え,
を考え,
![]() を
を
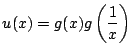 で定義する.
で定義する.
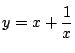 の整式
の整式 解答1
(1)
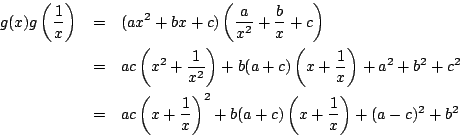
(2)
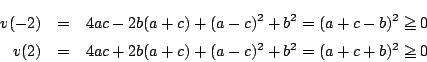
![]() ,または
,または![]() で
で
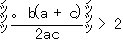 なら,
なら,
![]() で
で ![]() .
.
![]() でかつ
でかつ
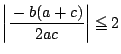 のときは,この条件の下で,
のときは,この条件の下で,
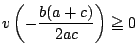 を示せばよい.
を示せばよい.
軸の条件は
![]() となるので
となるので
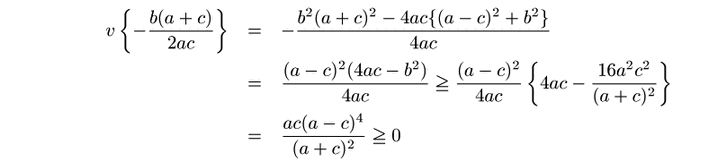
ゆえに題意が示された.□
注意
(2)は ![]() を
を ![]() で整理すると
で整理すると
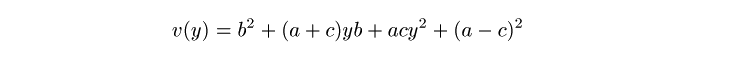
さて,より一般的な方法はないか.考えるヒントは
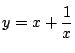 と置いたとき,
と置いたとき,
![]() になるような
になるような ![]() はどんなものかということだ.
それが判れば,
はどんなものかということだ.
それが判れば,
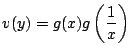 だから,
だから, ![]() の問題を
の問題を![]() の問題に還元できる.
の問題に還元できる.
解答2
(1)
![]() は明らかに
は明らかに ![]() と
と ![]() の対称式である.
したがってこれは基本対称式
の対称式である.
したがってこれは基本対称式 ![]() と
と ![]() の整式である.
の整式である.
![]() と
と ![]() で表したものの
で表したものの ![]() に
に ![]() を代入する.
を代入する.
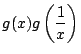 は
は
![]() と
と
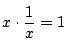 の整式となる.
つまり
の整式となる.
つまり
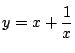 の整式として表せる.
の整式として表せる.
(2)
![]() の範囲
の範囲 ![]() を固定し
を固定し ![]() とする.
とする.
したがって
![]() の範囲のすべての
の範囲のすべての
![]() に対して
に対して ![]() であることが示された.□
であることが示された.□
このように考えれば, ![]() は二次式でなくても,一般の実数係数の多項式で成立する.
は二次式でなくても,一般の実数係数の多項式で成立する.
もう一つ考えよう.
例題 2.18 [01京府医大]
次の実数係数の三次式を ![]() とする.
とする.
まず ![]() が三次式であることをそのまま使う解を考えよう.
簡単のため必要に応じて
が三次式であることをそのまま使う解を考えよう.
簡単のため必要に応じて ![]() 等を
等を ![]() と書いてよい.
と書いてよい.
解答1
![]() の次数が異なる場合,
大きい方の次数を
の次数が異なる場合,
大きい方の次数を ![]() とすると
とすると
![]() は
は ![]() 次の整式である.恒等的に0ではあり得ない.
次の整式である.恒等的に0ではあり得ない.
![]() の次数が等しい場合,それを
の次数が等しい場合,それを ![]() 次として
次として
![]() ,
,
![]() と置く.このとき
と置く.このとき

解答2
![]() が定数でないとする.
が定数でないとする. ![]() は実数係数の整式なので,
は実数係数の整式なので,

次に
![]() とする.
とする.
![]() は整式なので,恒等的にこの解に等しい,つまり
は整式なので,恒等的にこの解に等しい,つまり![]() も定数である.□
も定数である.□
例題



