- (1)
- 1000から9999までの4桁の自然数のうち,1000や1212のようにちょうど 2種類の数字から成り立っているものの個数を求めよ.
- (2)
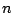 桁の自然数のうち,ちょうど2種類の数字から成り立っているものの個数を求めよ.
桁の自然数のうち,ちょうど2種類の数字から成り立っているものの個数を求めよ.
![]() 本のロープがあり,二つに折りにしてロープの端をそろえてある.
ロープの端をでたらめに二つずつ選んで結んでいき,1度結んだ端を2度選ばずに,
本のロープがあり,二つに折りにしてロープの端をそろえてある.
ロープの端をでたらめに二つずつ選んで結んでいき,1度結んだ端を2度選ばずに,
![]() 個の結び目を作る.
個の結び目を作る. ![]() 本のロープがすべてつながって一つの輪ができる確率を
本のロープがすべてつながって一つの輪ができる確率を ![]() とする.
とする.
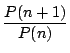 を求めよ.
を求めよ.
1から![]() までの番号が1つずつ書かれた
までの番号が1つずつ書かれた![]() 枚のカードがある.次の条件を満たすように左から右に
枚のカードがある.次の条件を満たすように左から右に![]() 枚を並べる場合の数を
枚を並べる場合の数を![]() とする.
とする.
以下の設問に答えよ.
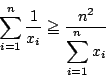
箱の中に1から ![]() までの番号が一つずつ書かれた
までの番号が一つずつ書かれた ![]() 枚のカードが入ってい
る.この箱から無作為にカードを 1 枚取り出して戻すという試行を
枚のカードが入ってい
る.この箱から無作為にカードを 1 枚取り出して戻すという試行を ![]() 回行う.
このとき,はじめから
回行う.
このとき,はじめから ![]() 回目
回目
![]() までに取り出したカードの番
号の和を
までに取り出したカードの番
号の和を ![]() とし,
とし,
![]() のうちのどれかが
のうちのどれかが ![]() となる確率を
となる確率を ![]() と
する.
と
する.
![]() は3以上の整数とする.数直線上で,座標が0の点を
は3以上の整数とする.数直線上で,座標が0の点を![]() とし,
座標が
とし,
座標が![]() の点を
の点を![]() とする.
とする.![]() をみたす整数
をみたす整数![]() を無作為に選び,
座標が
を無作為に選び,
座標が![]() の点を
の点を![]() ,座標が
,座標が![]() の点を
の点を![]() とする.
線分
とする.
線分
![]() のうちの最小値を
のうちの最小値を![]() とする.
とする.
![]() は自然数として,
は自然数として,