条件をみたす正の実数 ![]() が存在したとする.
が存在したとする.
とおく.このとき
が必要である.
逆に
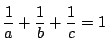 なら,任意の1でない正の実数
なら,任意の1でない正の実数
![]() に対して
に対して
![]() とおけば,この
とおけば,この![]() は条件をみたす.
したがって
は条件をみたす.
したがって
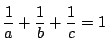 が,
が,![]() が存在
するための必要十分条件である.
が存在
するための必要十分条件である.
![]() より
より
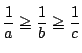 である.
である.
これから
![]() なら
なら ![]() は存在しない.
は存在しない.
![]() のとき
のとき
これから
![]() のとき
のとき
これから
ゆえに求める正の整数の組 ![]() は
は
□
条件をみたす正の実数 ![]() が存在したとする.
が存在したとする.
逆に
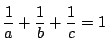 なら,任意の1でない正の実数
なら,任意の1でない正の実数
![]() に対して
に対して
![]() とおけば,この
とおけば,この![]() は条件をみたす.
したがって
は条件をみたす.
したがって
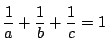 が,
が,![]() が存在
するための必要十分条件である.
が存在
するための必要十分条件である.
![]() より
より
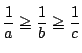 である.
である.
![]() なら
なら ![]() は存在しない.
は存在しない.
![]() のとき
のとき
![]() のとき
のとき
ゆえに求める正の整数の組 ![]() は
は
![]() に対し,
に対し,
![]() が十進法で表したとき
が十進法で表したとき![]() 桁の数で,その最高位の数字が1であるとする.
これは
桁の数で,その最高位の数字が1であるとする.
これは
![]() を固定するとき,これをみたす整数
を固定するとき,これをみたす整数![]() はちょうど一つある.
つまり桁が同じ数の中で最高位の数字が1であるものは一つだけある.
はちょうど一つある.
つまり桁が同じ数の中で最高位の数字が1であるものは一つだけある.
ただし,![]() が含まれていないので,与えられた数のうち1桁の数の中に最高位の数字が1で
あるものはない.
が含まれていないので,与えられた数のうち1桁の数の中に最高位の数字が1で
あるものはない.
![]() とすると
とすると
したがって求める数は603である. □
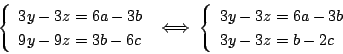
方程式(i)の解は,
実数![]() を用いて次のように表されるすべての
を用いて次のように表されるすべての![]() である.
である.
方程式
![]() なので,
なので,
![]() である.したがって
である.したがって
![]() から
から
ここで![]() とおく.
とおく.
![]() 平面の四分の一円
平面の四分の一円
![]() と直線
と直線![]() が共有点をもつ
が共有点をもつ![]() の最大値は
円と直線が接するときで
の最大値は
円と直線が接するときで![]() ,
最小値は
,
最小値は![]() を通るときで1.つまり
を通るときで1.つまり![]() の範囲は
の範囲は
![]() である.
逆にこの範囲の
である.
逆にこの範囲の![]() に対しては
に対しては![]() が存在する.
が存在する.
したがって解![]() のとる値の範囲は,
のとる値の範囲は,
![]() を
を![]() の二次方程式として整理すると
の二次方程式として整理すると
![]() .
.
ゆえに![]() が
が
![]() に解をもつ必要十分条件は
に解をもつ必要十分条件は
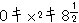 .
.
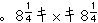
点![]() を原点にして
を原点にして
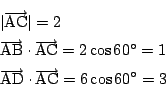
次に
![]() とする.条件から
とする.条件から
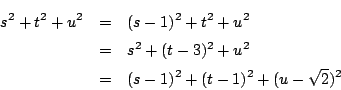
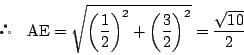
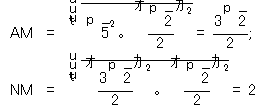
また
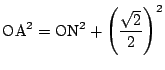 より
より
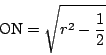
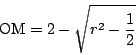
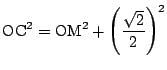 より
より
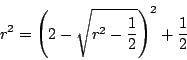
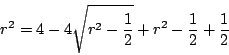
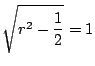 である.
である.
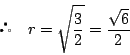
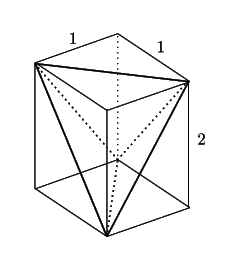 別解
別解
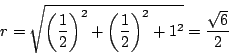
![]() の3頂点
の3頂点
![]() の
対辺の長さを
の
対辺の長さを![]() とする.また点
とする.また点![]() の位置ベクトルを
の位置ベクトルを
![]() の
ように表す.
の
ように表す.
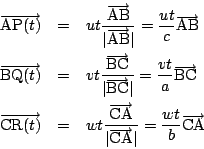
![]() はそれぞれの辺を頂点から頂点まで移動するのにかかる時間が等しいことを意味している.
つまり,3点が同時に次の頂点に到達することを意味している.
よって題意が示された.
□
はそれぞれの辺を頂点から頂点まで移動するのにかかる時間が等しいことを意味している.
つまり,3点が同時に次の頂点に到達することを意味している.
よって題意が示された.
□
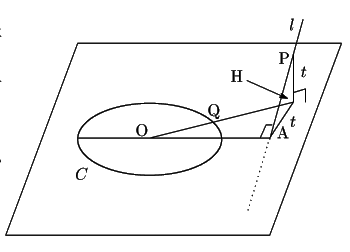
![]() 上の点
上の点 ![]() で,点
で,点 ![]() との距離が最小になるものは,
との距離が最小になるものは,
![]() と円
と円 ![]() の中心
の中心 ![]() を結ぶ直線が最初に
を結ぶ直線が最初に ![]() と交わる
点である.
と交わる
点である.
このとき
 のとき
のとき 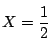 で
最小値
で
最小値
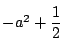 をとる.
をとる.
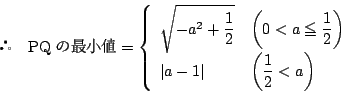
訂正:a=bのとき「最小値100bl」
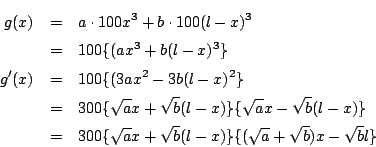
点![]() に対して,0か1を対応させる関数
に対して,0か1を対応させる関数![]() を次のように定める.
を次のように定める.
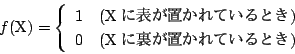
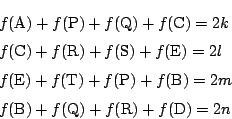
このとき
![]() の値も決まっている.この値を
の値も決まっている.この値を![]() とする.
すなわち
とする.
すなわち
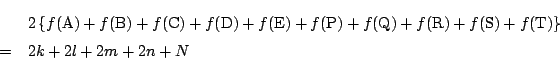
![]() の値を決めれば条件を満たす他の値の決め方がただ一通り存在するので,
条件を満たすような
A,B,C,D,E上へのコインの置き方は二通りある.
□
の値を決めれば条件を満たす他の値の決め方がただ一通り存在するので,
条件を満たすような
A,B,C,D,E上へのコインの置き方は二通りある.
□
1.
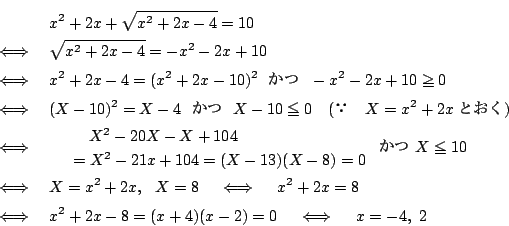
2.
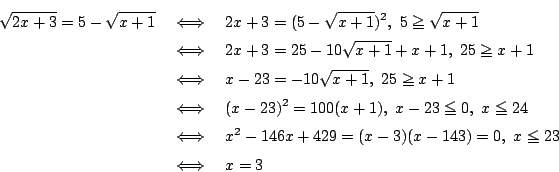
3.
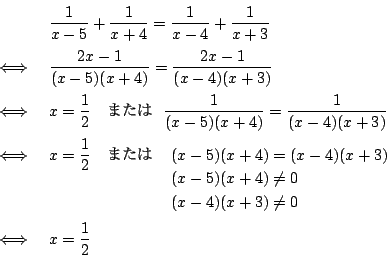
4.
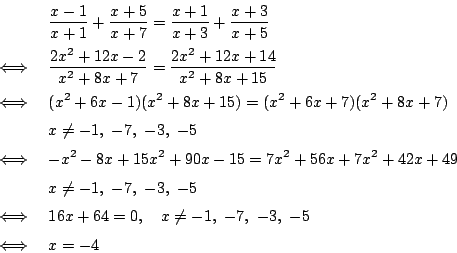
5.
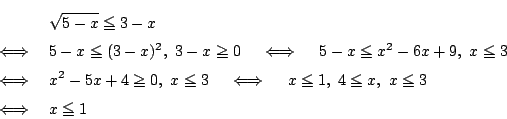
6.

基準点 ![]() をとり,
直線
をとり,
直線 ![]() 上の点
上の点 ![]() と
直線
と
直線 ![]() 上の点
上の点 ![]() を
を
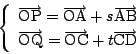
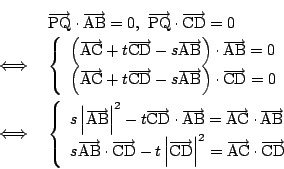
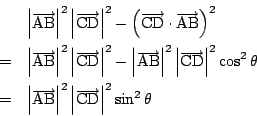
連立式を2直線の式と考えれば,平行条件が否定されたので必ず交わる.
あるいは,連立一次方程式の行列の行列式が0でない.
つまり![]() と
と ![]() に関する連立一次方程式がただ一組の解をもつことを意味している.
□
に関する連立一次方程式がただ一組の解をもつことを意味している.
□
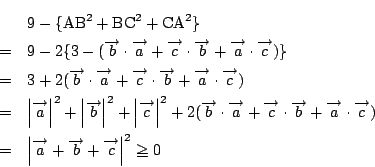
別解
![]() も同樣である.
も同樣である.
![]() の外接円の半径が1なので,
正弦定理から
の外接円の半径が1なので,
正弦定理から
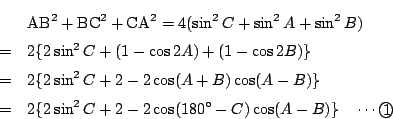
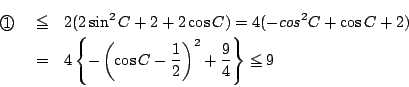
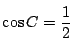 ,
つまり
,
つまり
各頂点
![]() の内角を
の内角を
![]() とする.
とする.
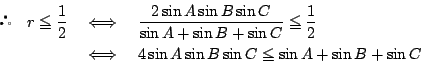
ここで和積,積和の公式と![]() およびその類似の等式を用いて右辺を変形する.
およびその類似の等式を用いて右辺を変形する.
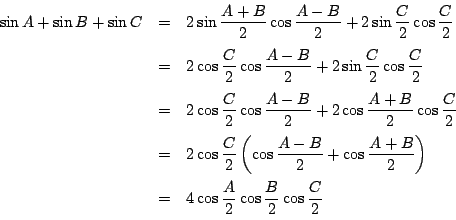
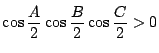 なので,
なので,
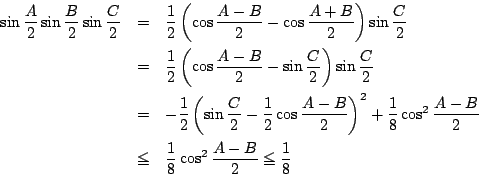
一部別解
解法のなかの不等式
![]() なので相加平均・相乗平均の不等式から
なので相加平均・相乗平均の不等式から
三点
![]() ,
,
![]() ,
,
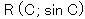 をとるとその重心
をとるとその重心
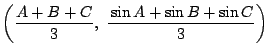 は
は
![]() の内部にある.
の内部にある.![]() のグラフが対応する区間では上に凸なので,
のグラフが対応する区間では上に凸なので,![]() の三辺は領域
の三辺は領域![]() にあり,その結果,重心も領域
にあり,その結果,重心も領域![]() にある.
これから
にある.
これから
別解1
![]() の頂点の対辺の長さを
の頂点の対辺の長さを![]() とする.
また内心を
とする.
また内心を![]() とする.
さらに各点の外心
とする.
さらに各点の外心![]() を基準点とする位置ベクトルを
を基準点とする位置ベクトルを
![]() のように小文字で表す.
のように小文字で表す.
![]() は
は
![]() の二等分線なので,
の二等分線なので,
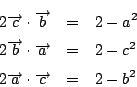
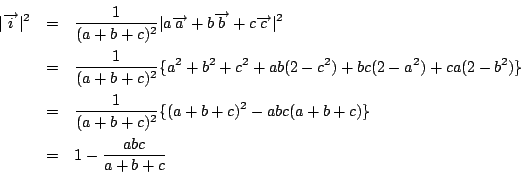
ここで正弦定理から![]() なので
なので
別解2
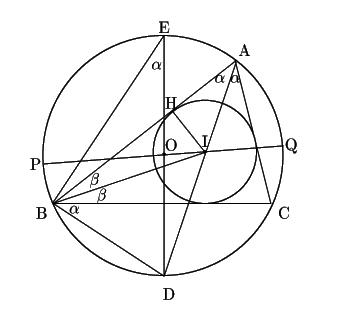 鈍角三角形や直角三角形では明らかに
鈍角三角形や直角三角形では明らかに
![]() なので,
なので,
![]() は鋭角三角形とする.
内心を
は鋭角三角形とする.
内心を![]() ,外心を
,外心を![]() とする.
とする.
![]() ,
,
![]() とおく.
とおく.
図のように,AIと外接円の交点をD,Dを通る直径をDEとする.
また内心Iから辺ABへの垂線の足をHとする.
さらに内心Iを通る直径をPQとする.
 で
で
![]() より,
より,
次に図のように
![]() なので
なので
別解3
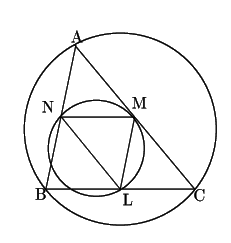 三角形の内接円の半径
三角形の内接円の半径![]() とは
とは
三角形の3辺と共有点をもつ円の半径の最小値である.
![]() は
は
![]() と相似で,相似比は
と相似で,相似比は![]() である.
つまり三辺と共有点をもち半径
である.
つまり三辺と共有点をもち半径![]() の円が存在する.
ゆえに,内接円の半径
の円が存在する.
ゆえに,内接円の半径![]() は
は![]() 以下である.
□
以下である.
□
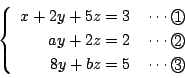
したがって
![]() を満たす
を満たす![]() と
と![]() が
ただ一つ定まればよい.
が
ただ一つ定まればよい.
![]() より
より
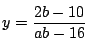 なので順次代入して次の解を得る.
なので順次代入して次の解を得る.
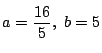 のときである.
このとき方程式
のときである.
このとき方程式
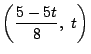 と表される.
このとき
と表される.
このとき
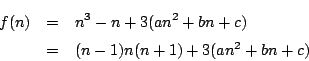
よって,すべての整数![]() に対して,
に対して,![]() は3の倍数である.
は3の倍数である.
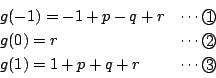
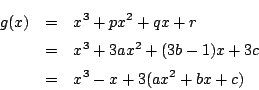
別解
(1)(2)あわせて解くこともできる.
![]() とおく.
すべての整数
とおく.
すべての整数![]() に対し
に対し![]() が3の倍数となることは,
が3の倍数となることは,
![]() が3の倍数,かつ
が3の倍数,かつ![]() が3の倍数であることと同値.
が3の倍数であることと同値.
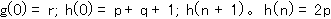
![]() とおけば,
とおけば,
![]() となる.
□
となる.
□
![]() とする.
このとき
とする.
このとき
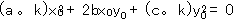 より
より
![]() なら
なら
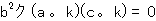 は成立している.
は成立している.
![]() のとき.2次方程式
のとき.2次方程式
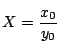 が存在したので,
が存在したので,
次に③が成り立っているとする.
![]() のときは,
のときは,
![]() が①の解である.
が①の解である.
![]() のとき.2次方程式②の判別式が負でないので,
2次方程式2に実数解が存在する.
それを
のとき.2次方程式②の判別式が負でないので,
2次方程式2に実数解が存在する.
それを ![]() とする.
このとき
とする.
このとき
つまり③のとき①に![]() 以外の解が存在した.
したがって与方程式に
以外の解が存在した.
したがって与方程式に
![]() 以外の解が存在するためには,
以外の解が存在するためには,
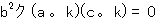 が成り立つことが必要十分である
ことが証明された.
が成り立つことが必要十分である
ことが証明された.
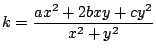 とおく.
求める
とおく.
求める 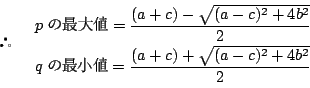
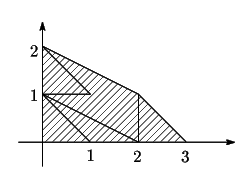 その上で点
その上で点![]() を動かすことにより,
を動かすことにより,
![]() は三角形
は三角形![]() の頂点
の頂点![]() が
三角形
が
三角形![]() 内にあるように動かした図形の全体になることがわかる.
内にあるように動かした図形の全体になることがわかる.
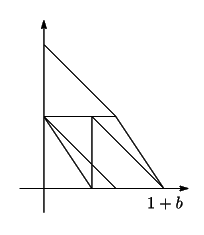
![]() のとき
のとき![]() は図の斜線部分である.
その面積は
は図の斜線部分である.
その面積は
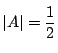 ,
,
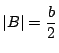 である.
である.
![]() のときは(1)と同様に
のときは(1)と同様に
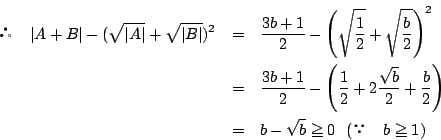
また,![]() のときは図のようになる.
よって
のときは図のようになる.
よって
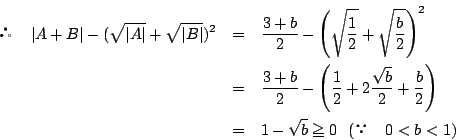
□
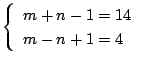 に整数解があればよい.これから
に整数解があればよい.これから
次に![]() をみたす
をみたす![]() の存在を示す.
の存在を示す.
![]() なので,
なので,
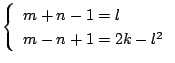 に自然数解があるように整数
に自然数解があるように整数![]() がとれることを示せばよい.
がとれることを示せばよい.
![]() と
と![]() について解いて
について解いて
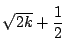 を超えない最大の整数とする.つまり
を超えない最大の整数とする.つまり
存在の別証明
次に![]() をみたす
をみたす![]() の存在を
の存在を![]() についての数学的帰納法で示す.
についての数学的帰納法で示す.
![]() のとき.
のとき.![]() より成立.
より成立.
![]() のとき
のとき![]() とし,
とし,![]() のときの存在を示す.
この
のときの存在を示す.
この![]() について.
について.
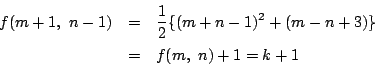
 であるから
であるから
解説
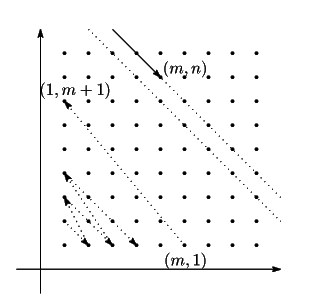 (3)後半の数学的帰納法による証明は次のことにもとづいている.
(3)後半の数学的帰納法による証明は次のことにもとづいている.
数学的帰納法の結果,
![]() が
が![]() からはじめて
からはじめて![]() 番目にあることが示されている.
番目にあることが示されている.
直接計算することもできる.![]() の上には
の上には![]() 個の格子点がある.
したがって,
個の格子点がある.
したがって,![]() は
は![]() からはじめて
からはじめて
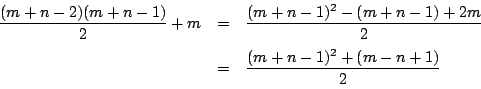
□
関数
![]() と
と
![]() のグラフの共有点の個数は
のグラフの共有点の個数は
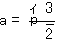 である.
である.
またそれぞれの放物線と直線が接するのは 判別式を調べて
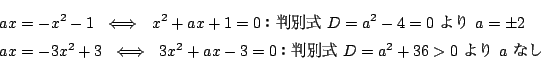
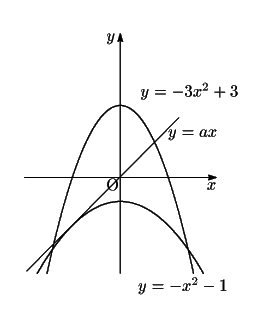
![]() 軸に関する対称性から
軸に関する対称性から![]() の範囲で共有点の個数は次のように決まる.
の範囲で共有点の個数は次のように決まる.
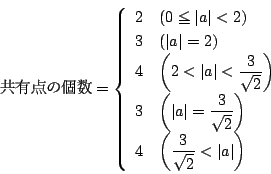
□
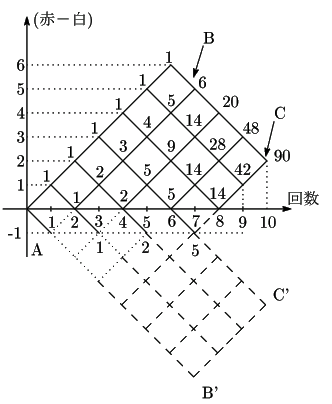
「赤の個数-白の個数」が-1になることなく点 ![]() になる場合の数,
つまり,
になる場合の数,
つまり, ![]() 上に来ることなく原点から点
上に来ることなく原点から点 ![]() に至る経路の総数を
に至る経路の総数を
![]() とする.
とする.
原点から点 ![]() に至る経路の総数は
に至る経路の総数は
![]() 通りある.
このうち
通りある.
このうち ![]() 上を通る経路の数を求める.
上を通る経路の数を求める.
![]() とし,
とし, ![]() で
折り返した点を
で
折り返した点を ![]() とする.
とする. ![]() 上を通る経路は,この折り返しで
原点から
上を通る経路は,この折り返しで
原点から ![]() に至る経路の総数と一致する.つまり
に至る経路の総数と一致する.つまり
![]() .
.
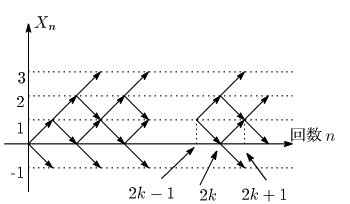 硬貨を投げる試行は各回独立で,1回の試行で表の出る確率と裏のでる確率は等しく
硬貨を投げる試行は各回独立で,1回の試行で表の出る確率と裏のでる確率は等しく
![]() とする.
とする.
![]() 軸の0と自然数値を「回数」に,
軸の0と自然数値を「回数」に, ![]() 軸を「数直線」にして,各回の試行の後,
駒がある点
軸を「数直線」にして,各回の試行の後,
駒がある点 ![]() の座標をとる.それぞれ原点を0にする.
このような図では表がでれば
の座標をとる.それぞれ原点を0にする.
このような図では表がでれば ![]() ,裏がでれば
,裏がでれば![]() と動き,その確率はいずれも
と動き,その確率はいずれも![]() である.
である.
奇数 ![]() に対して,
に対して, ![]() 回目に硬貨を投げたあと,
駒が点1に来るのは,最初表が出て点1に来て,その後,
2回ずつの試行で1から1に動くことを
回目に硬貨を投げたあと,
駒が点1に来るのは,最初表が出て点1に来て,その後,
2回ずつの試行で1から1に動くことを
![]() 回くり返すときのみである.
回くり返すときのみである.
また ![]() 回の試行の後に
回の試行の後に
![]() となる確率を
となる確率を ![]() と書くことにする.
と書くことにする.
さて駒が点1にあるとき,その後2回の試行で再び駒が1に来る確率は
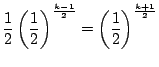
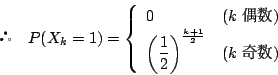
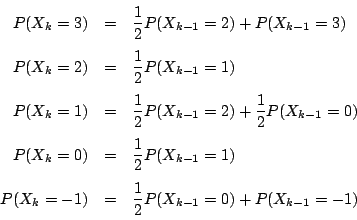
![\begin{eqnarray*}
∴ \quad E[X_k]
&=&3\cdot P(X_k=3)+2\cdot P(X_k=2)+1\cdot P(...
... +1\cdot P(X_{k-1}=1)+(-1)\cdot P(X_{k-1}=-1)\\
&=&E[X_{k-1}]
\end{eqnarray*}](images/img1246.gif)
別解1 (1)は(2)で作った関係式から求めてもよい.
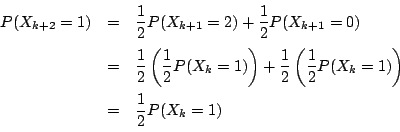
注意
(2)は図をもとに各
![]() に対する
に対する![]() と
と ![]() の相互の
関係式を作り,それをもとに期待値
の相互の
関係式を作り,それをもとに期待値![]() と
と![]() の漸化式を作ろうとした.
やってみれば結果として
の漸化式を作ろうとした.
やってみれば結果として
![]() になった.
になった.
なお,記号![]() は数Bでの記号であるが,定義して用いれば数Iで用いてよい.
また,この解答はあくまで数Iの範囲で解いている.
は数Bでの記号であるが,定義して用いれば数Iで用いてよい.
また,この解答はあくまで数Iの範囲で解いている.
数Bでならう期待値の加法性
![]() を用いれば次のように解くこともできる.
を用いれば次のように解くこともできる.
別解2
![]() 回目の試行で移動する量を
回目の試行で移動する量を ![]() とおく.これは確率変数である.そして
とおく.これは確率変数である.そして
そこで
![\begin{eqnarray*}
E[X_k]&=&E[r_1+r_2+\cdots+r_k]\\
&=&E[r_1]+E[r_2]+\cdots+E[r_k]
\end{eqnarray*}](images/img1261.gif)
![\begin{eqnarray*}
E[r_k]&=&p_{k-1}\cdot 0
+(1-p_{k-1}) \left(1\times\dfrac{1}{2}+(-1)\times\dfrac{1}{2} \right)\\
&=&0
\end{eqnarray*}](images/img1262.gif)
(1)
「白白白」から姶めて,3回の操作の結果,色の並び方が「黒白白」となる場合,「白黒白」
となる場合,または「白白黒」となる場合は同様に確からしい.したがって問題(2)の記号を用いれば,
求める確率は
![]() である.よって,(2)から先に解く.
である.よって,(2)から先に解く.
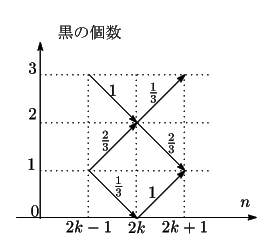 (2)
「白白白」から始めて,
(2)
「白白白」から始めて,![]() 回の操作の結果,黒の個数が1である確率が
回の操作の結果,黒の個数が1である確率が![]() である.
1回の試行で黒の個数の増減は1で奇数である.最初は黒の個数は0で偶数であったから,
黒の個数は,偶数回の試行の後は偶数個で0個か2個,奇数回の試行の後は奇数個で1個か3個である.
である.
1回の試行で黒の個数の増減は1で奇数である.最初は黒の個数は0で偶数であったから,
黒の個数は,偶数回の試行の後は偶数個で0個か2個,奇数回の試行の後は奇数個で1個か3個である.
![]() 回の操作の結果,黒の個数が3である確率を
回の操作の結果,黒の個数が3である確率を![]() とする.
とする.
![]() と
と![]() のときの
のときの![]() の漸化式を求める.図のように,個数の変化とその確率が定まる.
の漸化式を求める.図のように,個数の変化とその確率が定まる.
これから
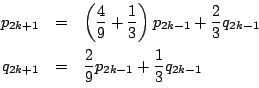
0でない数字を△とする.千の桁は△のみ.
他の三桁は0でも△でもよい.すべて△の場合のみ除く.
1つが0である場合.
6本の端の一つを任意に選ぶ. ![]() とする.残る5本の端のうち,
とする.残る5本の端のうち,
![]() か
か ![]() の端を選ぶ.
の端を選ぶ. ![]() とする.
さらに残る4本の端の一つを任意に選ぶ.それが
とする.
さらに残る4本の端の一つを任意に選ぶ.それが![]() か
か![]() の端なら
の端なら
![]() の2本の端を,
の2本の端を,![]() の端なら
の端なら![]() か
か![]() の
残る端を選ぶ.最後に残った2本の端を結ぶ.
の
残る端を選ぶ.最後に残った2本の端を結ぶ.
このとき一つの輪ができる.
 .
.
参考
題意の事象の起こる確率を![]() とすると,
とすると,

別解
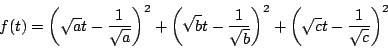
![]() となるのは
となるのは ![]() となる解があるとき.つまり
となる解があるとき.つまり
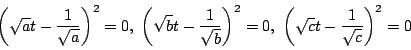
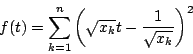
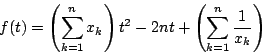
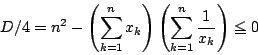
![]() となるのは
となるのは ![]() となる解があるとき.つまり
となる解があるとき.つまり

注意 別解はコーシー・シュワルツの不等式の証明法そのものである.
![]() の場合に,一般化できるような方法をさがしておくことが大切である.
□
の場合に,一般化できるような方法をさがしておくことが大切である.
□
![]() ということは
ということは![]() のみ.その確率は
のみ.その確率は![]() 枚中1のカードを引く確率.
枚中1のカードを引く確率.
![]() ということは,
ということは,![]() または,
または,
![]() .
.
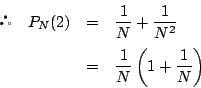
![]() ということは,
ということは,![]() ,
,
![]() または
または
![]() .
.
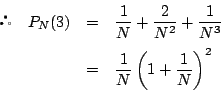
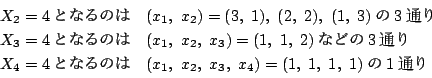
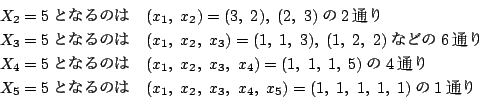
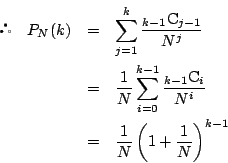
線分
![]() の長さをそれぞれ
の長さをそれぞれ![]() とおく.
条件を満たす
とおく.
条件を満たす![]() の組と,
の組と,
![]() である確率を
である確率を![]() ,
,![]() である確率を
である確率を![]() とおく.
とおく.
![]() となる事象の総数は
となる事象の総数は
![]() のときは
のときは![]() ,
,
![]() となるのは
となるのは![]() の1通りなので
の1通りなので
![]() のとき.
のとき.
![]() で
で
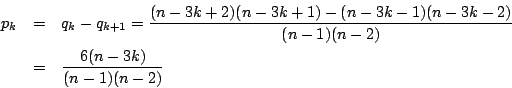
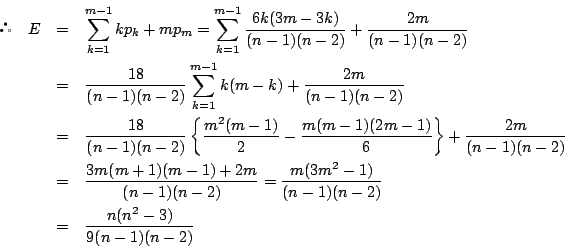
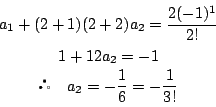
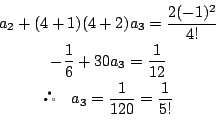
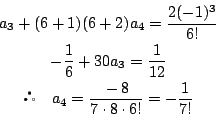
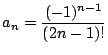 と推測される. これを数学的帰納法で示す.
と推測される. これを数学的帰納法で示す.
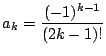 で成立するとする.
このとき,条件式を
で成立するとする.
このとき,条件式を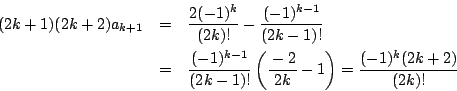
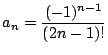 が成立する.
が成立する.
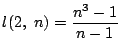 であり,
であり,
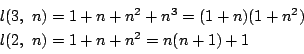
以下![]() は正整数とする.
は正整数とする.
![]() と表されるとき.
と表されるとき.
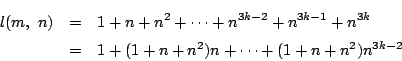
![]() と表されるとき.
と表されるとき.
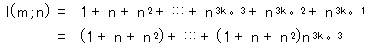
![]() と表されるとき.
と表されるとき.
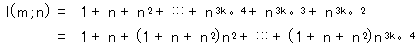
![]() と
と![]() は互いに素なので,
は互いに素なので,![]() と
と![]() は互いに素.
は互いに素.
ゆえに「どんな![]() に対しても
に対しても
![]() または
または
![]() が成り立つ」という命題は正しい.
□
が成り立つ」という命題は正しい.
□