整数問題などでは, 条件を満たすすべての整数や整数の組を求める問題では, 何らかの必要条件で範囲を絞ることが出来れば, その範囲にある整数は有限個となり, 後は一つ一つ調べるという方法が基本である.
![]() をみたすすべての
をみたすすべての ![]() に対して
に対して
![]() が成り立つために,定数
が成り立つために,定数 ![]() がみたすべき条件を求めよ.
がみたすべき条件を求めよ.
考え方
一定の条件を満たすすべての ![]() と
と ![]() に対してつねに成立する条件を求めよ
ということだが,すべてで成立するものを直接さがすのは困難なときがある.
に対してつねに成立する条件を求めよ
ということだが,すべてで成立するものを直接さがすのは困難なときがある.
そのときどうするか.いくつかの特別な ![]() と
と ![]() の値で試してみるだろう.
条件を決めるべき定数は
の値で試してみるだろう.
条件を決めるべき定数は ![]() と
と ![]() の二つなのだから,二組の
の二つなのだから,二組の ![]() と
と ![]() の値
で試せばある程度のことはわかる.
の値
で試せばある程度のことはわかる.
それから逆にその条件の下でつねに成立することを示せばよい.それが次の解答だ.
解答
![]() のとき
のとき
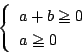


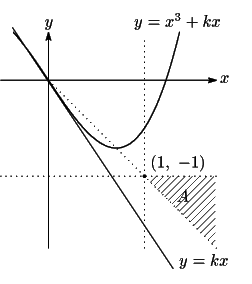
例題 1.5 [99京大後期文系]
3次関数 ![]() のグラフを考える. 連立不等式
のグラフを考える. 連立不等式
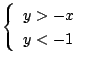 が表す領域を
が表す領域を ![]() とする.
とする.
![]() のどの点からも上の3次関数のグラフに接線が3本引けるための,
のどの点からも上の3次関数のグラフに接線が3本引けるための,
![]() についての必要十分条件を求めよ.
についての必要十分条件を求めよ.
その上で,領域![]() がそこに含まれるための
がそこに含まれるための![]() に関する条件を求める.
そのときに,必要条件で絞り,それが十分条件でもあることを示すのである.
に関する条件を求める.
そのときに,必要条件で絞り,それが十分条件でもあることを示すのである.
解答
![]() とする.
とする.
![]() 平面上の点
平面上の点![]() から
から![]() へ3本の接線が引けるために,
へ3本の接線が引けるために,
![]() が満たすべき条件を求める.
点
が満たすべき条件を求める.
点![]() から
から![]() への接線の接点の
への接線の接点の![]() 座標を
座標を![]() とする.
とする.
![]() から,
から,![]() の
の![]() 上の点における接線は
上の点における接線は
求めるべき![]() の条件は
の条件は![]() となることである.
領域
となることである.
領域 ![]() が第4象限にあるので,
が第4象限にあるので,![]() の点の
の点の![]() 座標は正である.
座標は正である.
![]() が正のとき
が正のとき![]() なので,
なので,
![]() のうち
のうち![]() 座標が正の領域は
座標が正の領域は
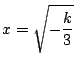 であるが,
であるが,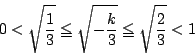
求める必要十分条件は![]() である.
□
である.
□