![]() を整数とする.「方程式
を整数とする.「方程式 ![]() が整数解
が整数解 ![]() をもつ」
ためには,
をもつ」
ためには, ![]() が奇数または4の倍数であることが,必要かつ十分条件であることを示せ.
が奇数または4の倍数であることが,必要かつ十分条件であることを示せ.
解答
整数解をもつとする.それを
![]() とする.すると,
とする.すると,
これは整数解をもつような ![]() が「奇数または4の倍数」に絞られたのだ.
が「奇数または4の倍数」に絞られたのだ.
![]() は
は![]() ではあり得ないことがわかったのだ.
ではあり得ないことがわかったのだ.
逆に,
![]() のときは
のときは
![]() のときは
のときは
例題 1.7 [84東京工大]
![]() を正の整数とする.
を正の整数とする.
必要条件で絞る方法を用いる整数問題の典型だ. どのような必要条件を用いるか.それが小問でヒントとして与えられている. そこで用いられているのは実数条件だ. 実数条件だけでも素数が二つに限定されるのだ.
解答
(1)
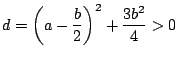 であるから,
であるから,
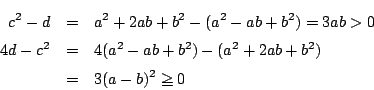
(2)
![]() が素数のべきになったとしてそれを
が素数のべきになったとしてそれを
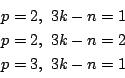
![]() のとき.
のとき.![]() である.
したがって
である.
したがって
![]() となる.
このとき
となる.
このとき
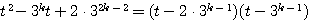 より
より
以上から
例題 1.8 [01京大理系]
整数 ![]() に対し
に対し
考え方
この問題はどうだろうか.
「どこから手をつけていいかわかりにくい」という声が聞こえる.
そのときは ![]() を同値変形で解きほぐすのだ.
まず
を同値変形で解きほぐすのだ.
まず![]() は連続二数の積なので必ず整数になる.
は連続二数の積なので必ず整数になる.![]() は
は
解答
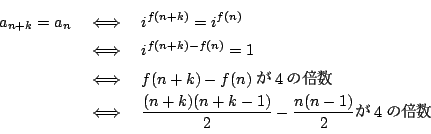
※ こうなればもう複素数を離れて,整数の問題になった.
![]() のとき
のとき
![]() .
. ![]() と
と ![]() は奇数偶数が逆なので,
整数
は奇数偶数が逆なので,
整数 ![]() を用いて
を用いて![]() か
か ![]() と書けることが必要.
と書けることが必要.
![]() のとき
のとき
![]() .
.
![]() と
と![]() は奇数偶数が逆なので
は奇数偶数が逆なので![]() か
か![]() と書けることが必要 .
両方成立するのは
と書けることが必要 .
両方成立するのは ![]() .つまり
.つまり ![]() が必要.
が必要.
逆に ![]() なら
なら![]() は8の倍数になる.
は8の倍数になる.