- 整式
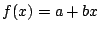 を考える.任意の整数
を考える.任意の整数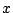 に対して,
に対して,
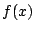 が整数であるための必要十分条件は「
が整数であるための必要十分条件は「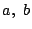 がともに整数である」ことを示せ.
がともに整数である」ことを示せ.
- 整式
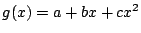 を考える.任意の整数
を考える.任意の整数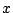 に対して,
に対して,
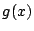 が整数であるための必要十分条件は「
が整数であるための必要十分条件は「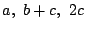 のすべてが整数である」ことを示せ.
のすべてが整数である」ことを示せ.
- 整式
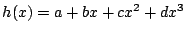 を考える.任意の整数
を考える.任意の整数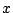 に対して,
に対して,
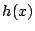 が整数であるための必要十分条件は「
が整数であるための必要十分条件は「
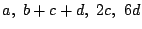 のすべてが整数である」ことを示せ.
のすべてが整数である」ことを示せ.
次の例題を二通りの方法でやってみよう.
例題 1.9 [05大教大]
解法1
十分条件であることを示す.
![]() とおくと
とおくと
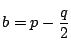 ,
,
![]() より
より
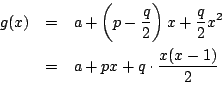
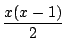 は整数なので,
すべての整数
は整数なので,
すべての整数十分条件であることを示す.
![]() とする.
とする.
![]() ,
,
![]() ,
,
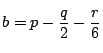 なので,
なので,
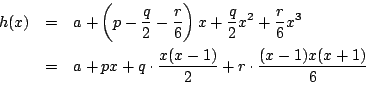
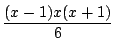 は整数なので,
すべての整数
は整数なので,
すべての整数解法2
よって![]() のとき
のとき
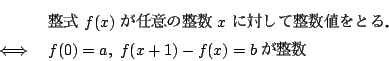
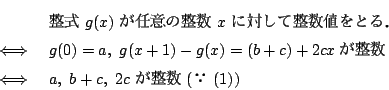

(上2行目 「3dx2」を「3dx3」に訂正).
である.