漸化式
![]() で定まる
整 数列
で定まる
整 数列 ![]() を考える.
を考える.
- (1)
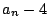 が7で割り切れることを証明せよ.
が7で割り切れることを証明せよ.
- (2)
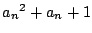 が
が 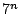 で割り切れることを証明せよ.
で割り切れることを証明せよ.
- (3)
- 正整数
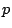 について,
について, 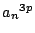 を
を 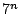 で割った余りを求めよ.
で割った余りを求めよ.
漸化式
![]() で定まる
整 数列
で定まる
整 数列 ![]() を考える.
を考える.
![]() を自然数とし,
を自然数とし,![]() の関数
の関数![]() を
を
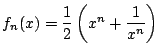 で定める.
で定める.
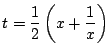 とすると,
とすると,
![]() は正の整数とし,二次方程式
は正の整数とし,二次方程式 ![]() の二つの実数解を
の二つの実数解を ![]() とする.
とする.
![]() とおくとき,すべての正の整数
とおくとき,すべての正の整数 ![]() について
次のことがなりたつことを示せ.
について
次のことがなりたつことを示せ.
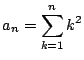 とおく.自然数
とおく.自然数 ![]() に対して
に対して
実数 ![]() に対して関数
に対して関数 ![]() を
を
![\begin{eqnarray*}
f_1(x)=f(x),&f_{n+1}(x)=f(f_n(x)),\\
d_1(x)=[\beta x],&d_{n+1}(x)=[\beta f_n(x)]
\end{eqnarray*}](images/img393.gif)
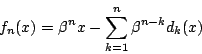
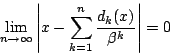
関数
![]() を次のように定める.
を次のように定める.
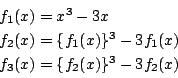
このとき以下の問いに答えよ.
![]() は
は ![]() の係数が1である
の係数が1である ![]() の
の ![]() 次式である.
相異なる
次式である.
相異なる ![]() 個の有理数
個の有理数
![]() に対して
に対して
![]() がすべて有理数であれば,
がすべて有理数であれば,
![]() の係数はすべて有理数であることを,数学的帰納法を用いて示せ.
の係数はすべて有理数であることを,数学的帰納法を用いて示せ.