
 ��: �_�̐��i
�O: �l����
��: �_�̐��i
�O: �l����
�� 1.2
���
1.2
�ȉ� 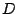 �͔��ʎ���\���D
�͔��ʎ���\���D
-
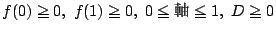 ���C
���C
-
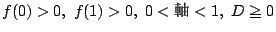 ���C
���C
- 1����
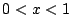 �ɂ���C�܂�
�ɂ���C�܂�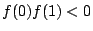 ���C
1����0�ő��̉���
���C
1����0�ő��̉���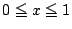 �ɂȂ��C�܂���
1����1�ő��̉���
�ɂȂ��C�܂���
1����1�ő��̉���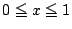 �ɂȂ���悢�D
�ɂȂ���悢�D
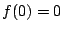 �̂Ƃ�
�̂Ƃ�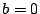 �ő��̉���
�ő��̉��� 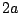 �D
�D
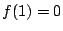 �̂Ƃ�
�̂Ƃ� 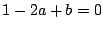 �ő��̉���
�ő��̉��� 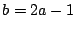 �D
�D
�䂦��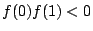 �C
�C
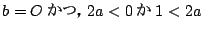 �܂���
�܂���
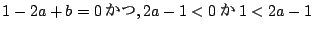
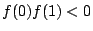 �܂�
�܂�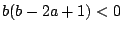
- (1)�����(3)�ł���D
�������C
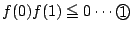 �܂���
�܂���
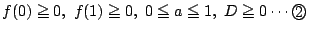 �ł悢�D
�@�ƇA��
�ł悢�D
�@�ƇA�� 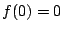 ��
�� 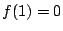 �̏ꍇ����d�ɓ����Ă��邪�C�u�܂��́v
�Ȃ̂ł��܂�Ȃ��D�䂦��
�̏ꍇ����d�ɓ����Ă��邪�C�u�܂��́v
�Ȃ̂ł��܂�Ȃ��D�䂦��
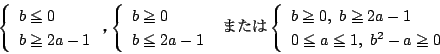
(a
2-b �ɒ���)
- (2)�C�܂���(4)�D�䂦��
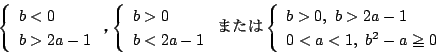
(a
2-b �ɒ���)
��
�� 1.3
���
1.3
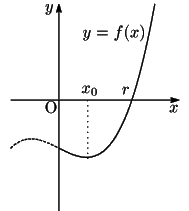
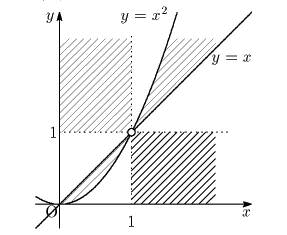 ��̏�������
��̏�������  �����
�����  �D���̂Ƃ�
�D���̂Ƃ� 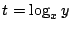 �Ƃ����D
�Ƃ����D
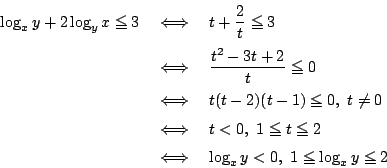
�@�@(�C�͂܂��͂ł���)
����������
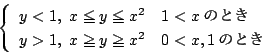
�@(0<x1�ɒ���)
���̗̈�͎��}�̂悤�ɂȂ�D
��
�� 1.5
���
1.5
�ł��邩��C��ϕ��̋���1�����邩�͂���Ȃ����ŁC�ϕ��v�Z���ς��D
���ꂼ���Βl���̒�ϕ����v�Z����ƁC
������ �̂Ƃ�
�̂Ƃ�
 �ł��邩��
�ł��邩��
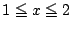 �̂Ƃ�
�̂Ƃ�
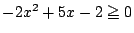 �ł��邪�C
�ł��邪�C
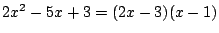 �Ȃ̂�
�Ȃ̂�
�ƂȂ�D���킹��
���������� 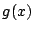 ��
��
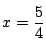 �ōő�l
�ōő�l 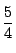 ���Ƃ�D
��
���Ƃ�D
��
�� 1.6
���
1.6
-
- (1)
- �������̏��ɏ����o���D
- (2)
- 1�̈ʂ�3�ʂ�C
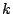 �̈ʂ�
�̈ʂ� 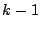 �̈ʂƂ͈قȂ鐔�Ȃ̂�2�ʂ�D
�̈ʂƂ͈قȂ鐔�Ȃ̂�2�ʂ�D
- (3)
 �@(
�@(
 )
)
 �ɂ��āD
�ɂ��āD
 �@(
�@( )
)
 �@(
�@(
 )
)
 �̂Ƃ��D����
�̂Ƃ��D����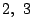 ��u���ꏊ��\���D1��1�ŋ��܂ꂽ�Ƃ���͂˂�
��u���ꏊ��\���D1��1�ŋ��܂ꂽ�Ƃ���͂˂�
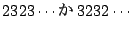 ��2�ʂ�D1�̈ʒu�ŕ��ނ���D
��2�ʂ�D1�̈ʒu�ŕ��ނ���D
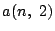 �ɂ��āD���l��1�̈ʒu�ŕ��ނ���D
�ɂ��āD���l��1�̈ʒu�ŕ��ނ���D
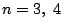 �ł��K����D�܂����炩��
�ł��K����D�܂����炩��
- (4)
- ���l��1�̈ʒu�ŕ��ނ���D
��
�� 1.7
���
1.7
-
- (1)
- �e�O���[�v�͎��R�����琬��C���v�f�͓���������Ȃ��Ă���D
������������
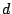 �͎��R���ł���D
�͎��R���ł���D
�O���[�vA�ɁC���R��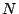 ��
��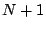 ���܂܂�Ă���Ƃ���D���̓̍���1�Ȃ̂ŁC
������1�ł���D�䂦��A�ɂ�
���܂܂�Ă���Ƃ���D���̓̍���1�Ȃ̂ŁC
������1�ł���D�䂦��A�ɂ�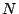 �ȏ�̑S�Ă̎��R����������D
�ȏ�̑S�Ă̎��R����������D
��ȏ�̃O���[�v�ɕ������̂ŁC
���̊e�O���[�v��1����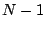 �܂ł̐��łł��Ă��Ȃ���Ȃ�Ȃ��D
�܂ł̐��łł��Ă��Ȃ���Ȃ�Ȃ��D
����́C�e�O���[�v�������ɑ����̎��R�����܂ނ��Ƃɔ�����D
����Ċe�O���[�v�͘A��2�������܂ނ��Ƃ͂Ȃ��D
- (2)
- �����ꂩ�̃O���[�v��1���܂ށD�O���[�vA��1���܂܂��Ƃ���D
�����(1)����A��2���܂܂Ȃ��D2��B�Ɋ܂܂��D�����3��B�Ɋ܂܂ꂸA�Ɋ܂܂��D
A��1��3���܂�2�͊܂܂Ȃ��̂ŁC������2�D���l��B��2��4���܂�3�͊܂܂Ȃ��̂Ō�����2�D
�����A�͊�CB�͋����̏W���ɂȂ�D
���̂悤�ȃO���[�v������1�ʂ�ł���D
- (3)
- 1�C3��A�ɁC2��B�ɂ��ꂼ������Ă���̂ŁC4��A�ɂ͊܂܂�Ȃ��D
����B�Ɋ܂܂��Ƃ���ƁCB��������2�ƂȂ�B�����ׂĂ̋������܂ނ��ƂɂȂ��C
�O�̃O���[�v�����ɂ͂Ȃ�Ȃ��D
�����4��C�Ɋ܂܂��D
A��1��3���܂ނ̂Ō�����2�Ŋ�̏W���ɂȂ�D�����5��A�Ɋ܂܂��D
B��C�͂��ꂼ���������Ȃ�D����6��C�Ɋ܂܂��ƁC
C�̌�����2�ƂȂ�CC��4�ȏ�̂��ׂĂ̋������܂ށD
�����B�������ɑ����̎��R�����܂ނ��Ƃɔ�����D
�䂦��6��B�ɓ���D
- (4)
- 1��2�͕ʂ̃O���[�v�ɂȂ�D�����A��B�Ƃ���D
3��A�ɂ͂���ꍇ�D(3)�Ŏ������悤�ɁCA�͊�̏W���D
B��C�͋����̏W���ł��������̏W���ɘA�������̋��������邱�Ƃ͂Ȃ��D
����Ă��̏ꍇ��B��
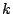 �����R���Ƃ���
�����R���Ƃ���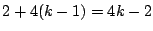 �C
C��
�C
C��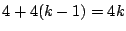 �̌`�������������Ȃ�D
���̏ꍇ��1�ʂ�ł���D
�̌`�������������Ȃ�D
���̏ꍇ��1�ʂ�ł���D
3��C�Ɋ܂܂��ꍇ�D4��B�ɓ����B�͂��ׂĂ̋����D
5��C�ɓ����C��3�ȏ�̂��ׂĂ̊���܂ނ̂�A���L���ɂȂ�D
�����5��A�ɓ���7��C.��������A��C��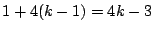 ��
��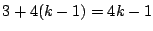 �̊���Ȃ�D
�̊���Ȃ�D
3��C�Ɋ܂܂�C4��A�ɓ���ꍇ�DA�͌�����3��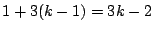 �̌`�̐����Ȃ�C����7���܂ށD
5��C�ɓ����C��3�ȏ�̂��ׂĂ̊���܂ނ̂�A��7���܂ނ��Ƃɔ�����D
�����5��B�ɓ���B��
�̌`�̐����Ȃ�C����7���܂ށD
5��C�ɓ����C��3�ȏ�̂��ׂĂ̊���܂ނ̂�A��7���܂ނ��Ƃɔ�����D
�����5��B�ɓ���B��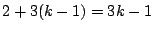 �̌`�̐����Ȃ�D
���̌��ʁC6��C�ɓ���CC��
�̌`�̐����Ȃ�D
���̌��ʁC6��C�ɓ���CC��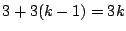 �`�̐����Ȃ�D
�`�̐����Ȃ�D
�䂦�Ɏ��R���S�̂��O�̃O���[�v�ɕ�����Ƃ��́C���̕������͎���3�ʂ�ł���D
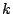 �͔C�ӂ̎��R����\���D
�͔C�ӂ̎��R����\���D
��
�� 1.10
���
1.10
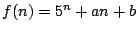 �Ƃ����D
�Ƃ����D
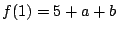 �C
�C 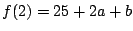 ���Ƃ���
16�̔{���ł��邱�Ƃ��K�v�ł���D
���Ƃ���
16�̔{���ł��邱�Ƃ��K�v�ł���D
�]����
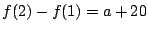 ��16�̔{���łȂ���Ȃ�Ȃ��D
��16�̔{���łȂ���Ȃ�Ȃ��D
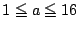 ���
���
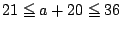 �D���͈̔͂�16�̔{����32�̂݁D
�䂦��
�D���͈̔͂�16�̔{����32�̂݁D
�䂦�� 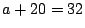 ���
��� 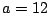 ���K�v�D
���K�v�D
����ɂ��̂Ƃ� 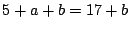 �D���l�ɍl��
�D���l�ɍl�� 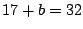 �ŁC
�ŁC  ���K�v�ł���D
���K�v�ł���D
�t��  �̂Ƃ�
�̂Ƃ�  �ɂ��Ă�
�ɂ��Ă� 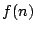 ��16�̔{���ł��邱�Ƃ������D
��16�̔{���ł��邱�Ƃ������D
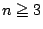
�Ȃ̂ł���������16�̔{���ł���D
�]���Ă��̏ꍇ�� 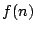 ��16�̔{���ł���D
��16�̔{���ł���D
�䂦�ɋ��߂� 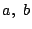 ��
�� 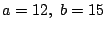 �D
�D

�ʉ�
������
�͂˂�16�̔{���ɂȂ邩��C
���߂������  ��16�̔{���ł��邱�ƂƓ��l�ł���D
��16�̔{���ł��邱�ƂƓ��l�ł���D
�܂�  ��
��
�� 1.11
���
1.11
 �̂Ƃ��ɐ������邱�Ƃ��K�v�ł���D
�̂Ƃ��ɐ������邱�Ƃ��K�v�ł���D
�܂�
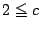
���K�v�ł���D
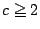 �̂Ƃ�
�̂Ƃ� 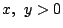 �Ȃ̂�
�Ȃ̂�
�ƂȂ�D�䂦��
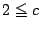
�͏\�������ł�����D
���������ċ��߂�  �͈̔͂�
�͈̔͂� �D
�D
�ʉ�1
 �Ȃ̂�
�Ȃ̂�
 �Ƃ����D
�Ƃ����D
�ł���D
�Ƃ����D
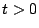
�̂Ƃ����
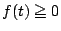
�ƂȂ�
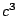
�͈̔͂����߂�D
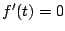
�ƂȂ�̂�
![$1+t=\sqrt[3]{c^3}t$](images/img810.gif)
�̂Ƃ��̂݁D
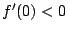
�Ȃ̂ł��̂Ƃ�
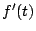
�͕����琳�ɕς��D
�䂦��
![$t=\dfrac{1}{\sqrt[3]{c^3}-1}>0$](images/img813.gif)
�ŋɏ����ŏ��D
���������ċ��߂�
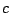
�͈̔͂�
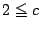
�D
�ʉ�2
��III��p����D
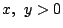 �Ȃ̂�
�Ȃ̂�
�ł���D
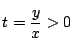
�Ƃ��āC
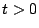
�̂Ƃ��˂�
�ƂȂ�悤��
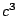
�͈̔͂́C
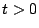
�ɂ�����
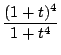
�̍ő�l�ȏ�͈̔͂ł���D
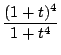 �̍ő�l�����߂�D
�̍ő�l�����߂�D
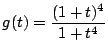 �Ƃ���D
�Ƃ���D
�ƂȂ�D�䂦��
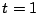
�̂Ƃ��ɑ傩�ő�ł���D�ő�l
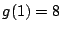
.
���������ċ��߂� 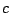 �͈̔͂�
�͈̔͂�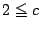 �D
��
�D
��
���̑��ʉ𑽐��DPDF�Q�Ƃ��ĉ������D
�� 1.12
���
1.12
�ł��邩��C��ӂ��݂������߂ɂ�,
������

�ɑ������ł��邱�Ƃ��K�v�\�������ł���.
�K�v���������߂�D
�A���
�������D���̂Ƃ��@���
��3�̔{���D
����
 �ƂȂ���
�ƂȂ���  �Ɋւ�������������Ȃ��̂ŁC
�Ɋւ�������������Ȃ��̂ŁC
 �ׂ��D
�ׂ��D
�t�ɁC ������,
������,  ��3�̔{���Ƃ���D���̂Ƃ�
��3�̔{���Ƃ���D���̂Ƃ�
���˂�
�͐����ɂȂ�D
�����͈̔͂ɂ��̏������݂��� 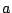 ��
�� 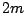 �Ƃ��.
�Ƃ��.
�e 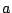 �ɑ��ď������݂���
�ɑ��ď������݂��� 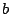 ��,
��,
�Ƃ��.
�����, 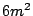 ��
�� 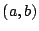 ������.
������.
�ʉ�
������

�ɑ������ƂȂ�K�v�\�������̋��ߕ��̕ʉ�.
�Ƃ���.
������,
����炪�����ł��邽�ߏ�����,
�ł���.
��
�� 1.13
���
1.13
�s��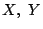 ��
��
�Ƃ����D
�ł���D���������ď���
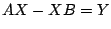
��
�Ɠ��l�ł���D
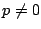 �ł���
�ł���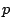 �ɑ���
�ɑ���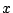 �����݂��邽�߂�
�����݂��邽�߂�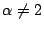 ���K�v�D
���K�v�D
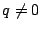 �ł���
�ł���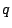 �ɑ���
�ɑ���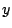 �����݂��邽�߂�
�����݂��邽�߂�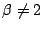 ���K�v�D
���K�v�D
������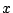 ��
��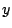 �ɑ�
�ɑ�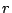 ��
��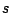 ��K���ɂƂ���
��K���ɂƂ���
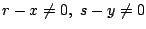 �Ƃ����Ƃ�
�Ƃ����Ƃ�
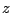 ��
��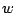 �����݂��邽�߂�
�����݂��邽�߂�
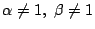 ���K�v�D
���K�v�D
�����
���K�v�D
�t�ɂ��̂Ƃ��C�ӂ�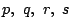 �ɑ���
�ɑ���
�ƂƂ邱�Ƃ��ł��C���炩���܂�
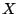
�͏���
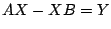
�����D
������
�͏\�������ł�����D
��
�� 1.14
���
1.14
�ƈ������������D���R��
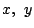
��p����
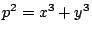
�ƕ\����悤�ȑf��
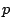
��
�ƂȂ�D
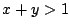
�ł��邩��C
�̂����ꂩ�ł���D
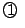 �̂Ƃ��D
�̂Ƃ��D
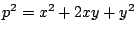 �Ȃ̂ŁC
�Ȃ̂ŁC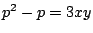 �D�����2��������
�D�����2��������
�͎�����
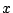
��
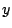
�����D���ʎ�
���K�v�ł���D���ꂩ��
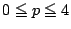
�D
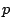
�͑f��������
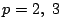
�ł���D
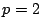
�Ȃ�C
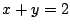
�D�����
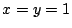
�D���̂Ƃ�
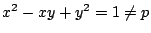
�D���Ȃ��D
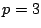
�Ȃ�C
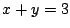
�D�����
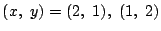
�D
���̂Ƃ�
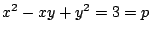
�D����͓K�ȉ��ł���D
 �̂Ƃ��D���l��
�̂Ƃ��D���l��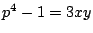 �D�����2��������
�D�����2��������
�͎�����
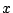
��
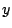
�����D���ʎ�
���K�v�ł���D���ꂩ��
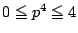
�D���̂悤��
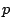
�͂Ȃ��D
�ȏ���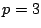 �C
�C
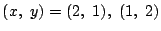 �D
��
�D
��
�� 1.15
���
1.15
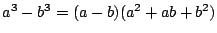 �ł���D������
�ł���D������
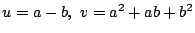 �Ƃ����D
�Ƃ����D
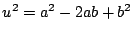 �ł��邩��
�ł��邩��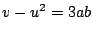 �D�܂�
�D�܂�
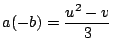 �D
�D
����������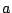 ��
��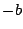 ��2��������
��2��������
�̓�̉��ł���D
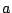
��
�͎����ł��邱�Ƃ��K�v�Ȃ̂ŁC���ʎ���
�Ƃ�����
���ꂩ��
 ��D
��D
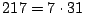 ��7��31�͑f���ł��邩��C
��7��31�͑f���ł��邩��C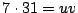 �ƂȂ�
�ƂȂ�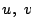 �̂����C
����
�̂����C
���� �������̂�
�������̂�
�ł���D���ꂼ��ɑ���
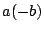
��-72��6�ł���D
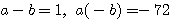 �̂Ƃ��C
�̂Ƃ��C ��
��
�̓�̉��D
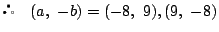
�D
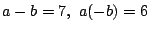 �̂Ƃ��C
�̂Ƃ��C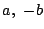 ��
��
�̓�̉��D
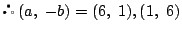
�D
��
�� 1.17
���
1.17
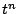 �̌W���𐄑����邽�߂ɂ�������
�̌W���𐄑����邽�߂ɂ�������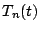 �����߂�D
�����߂�D
����������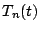 ��
��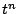 ���̌W����
���̌W����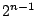 �Ɛ��������D������
�Ɛ��������D������
���Ƃ��C �Ɋւ��鐔�w�I�A�[�@�Ŏ����D
�Ɋւ��鐔�w�I�A�[�@�Ŏ����D
(i) 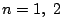 �̂Ƃ��́C��̂悤�ɐ�������D
�̂Ƃ��́C��̂悤�ɐ�������D
(ii) 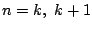 �̂Ƃ���
�̂Ƃ���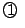 ����������Ƃ���D
����������Ƃ���D
�ƂȂ�D
���w�I�A�[�@�̉��肩��
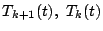 �͐����W���̐����Ȃ̂�
�͐����W���̐����Ȃ̂�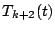 ��
�W���������ł���D�����
��
�W���������ł���D�����
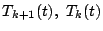 �̍ō����̍��̌W�����A�[�@�̉��肩���܂�̂ł�����܂߂Ă����̑�������������
�̍ō����̍��̌W�����A�[�@�̉��肩���܂�̂ł�����܂߂Ă����̑�������������
�ƂȂ�D����������
�ƂȂ�C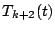 �͐����W����
�͐����W����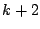 ��������
��������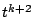 �̌W����
�̌W����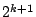 �ł��邱�Ƃ�
�����ꂽ�D�܂�
�ł��邱�Ƃ�
�����ꂽ�D�܂�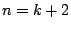 �ł�
�ł�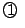 �����������D
�����������D
(iii)�@(i)(ii)��莩�R�� �ɑ���
�ɑ���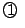 ����������D
����������D
-
�����藧���Ƃ𐔊w�I�A�[�@�Ŏ����D
(i) 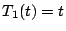 �Ȃ̂�
�Ȃ̂�
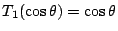 �C�܂�
�C�܂� �Ő����D
�����D
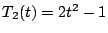 �Ȃ̂�
�Ȃ̂�
�܂�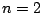 �Ő����D
�����D
(ii)  ��
��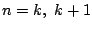 �Ő�������Ƃ���D
�Ő�������Ƃ���D ���
���
�����藧�D���w�I�A�[�@�̉���������Ă�����v�Z����D
����������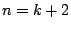 �ł����������D
�ł����������D
(iii)�@(i)(ii)��莩�R�� �ɑ���
�ɑ���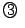 ����������D
����������D
��
�� 1.18
���
1.18
-
- (1)
- ���ƌW���̊W����
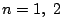 �̂Ƃ��D
�̂Ƃ��D
���Ƃ��ɐ����ŁC��������D
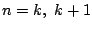 �Ő�������Ƃ���D���̂Ƃ�
�Ő�������Ƃ���D���̂Ƃ�
�ƂȂ�C����������Ȃ̂� 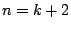 �ł���������D
�ł���������D
�䂦�ɂ��ׂĂ̐��̐���  �ɂ���
�ɂ���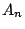 �͐����ł���D
�͐����ł���D
- (2)
-
(1)����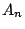 �͐����ł���D�䂦��
�͐����ł���D�䂦��
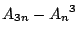 ��3�̔{���ł���D
��3�̔{���ł���D
��
�� 1.19
���
1.19
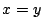 �̂Ƃ��͓�������������D
�̂Ƃ��͓�������������D
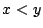 �Ƃ���D���̂Ƃ�
�Ƃ���D���̂Ƃ� 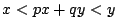 �ł���D
��
�ł���D
��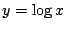 ����ɓʂȊ��ł��邩��C
����ɓʂȊ��ł��邩��C
�����藧�D���ꂩ��
��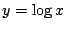 �͒P�������Ȃ̂�
�͒P�������Ȃ̂�
����������D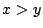 �̂Ƃ������l�Ȃ̂ŁC
�̂Ƃ������l�Ȃ̂ŁC
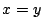 �̂Ƃ��Ƃ��킹�đ�ӂ̕s��������������D
����������
�̂Ƃ��Ƃ��킹�đ�ӂ̕s��������������D
���������� 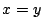 �̂Ƃ��ł���D
�̂Ƃ��ł���D
- (1)�Ɠ��l�ɍl���C
���������邱�Ƃ𐔊w�I�A�[�@�Ŏ����悢�D
 �̂Ƃ���(1)���琬���D
�̂Ƃ���(1)���琬���D
 �̏ꍇ�ɐ�������Ƃ�
�̏ꍇ�ɐ�������Ƃ�  �̏ꍇ�ɐ������邱�Ƃ������D
�̏ꍇ�ɐ������邱�Ƃ������D
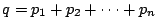 �Ƃ����D
�Ƃ����D
����сC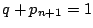 �ł��邱�Ƃɒ��ӂ���D
�ł��邱�Ƃɒ��ӂ���D
(�����F�ォ��2�s�ځC{}����1����2���̊Ԃ�+�}��)
�䂦��
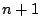
�̏ꍇ�����������D
����������

����
�܂�
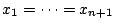
�̂Ƃ��D
����Ĉ�ʂ�  �ɑ��đ�ӂ������ꂽ�D��
�ɑ��đ�ӂ������ꂽ�D��
����
�̂Ƃ��C����͑������ςƑ��敽�ς̊W�̕s�����ł���D
��
�� 1.20
���
1.20
-
- (1)
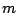 �Ɋւ��鐔�w�I�A�[�@�Ŏ����D
�Ɋւ��鐔�w�I�A�[�@�Ŏ����D
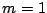 �̂Ƃ��D
�̂Ƃ��D
�ƂȂ�  �́C
�́C
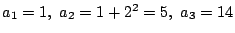 ���
��� 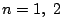 �Ɠ����D
�܂�
�Ɠ����D
�܂� 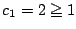 �Ő������Ă���D
����������D
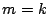 �̂Ƃ�
�̂Ƃ� 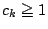 �Ƃ���D�܂�
�Ƃ���D�܂�
�ƂȂ�  �����Ȃ��Ƃ�����݂���Ƃ���D
����
�����Ȃ��Ƃ�����݂���Ƃ���D
����  �̂Ȃ��ōő�̂��̂�
�̂Ȃ��ōő�̂��̂� 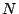 �Ƃ���D����������
�Ƃ���D����������
�ł���D
�����ł���
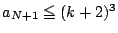 �������ꂽ��
�������ꂽ��
�ƂȂ�C
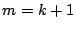 �̂Ƃ���
�̂Ƃ���
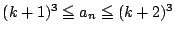 ���݂���
���݂���  ��
���Ȃ��Ƃ�����݂�
��
���Ȃ��Ƃ�����݂�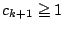 �ƂȂ邱�Ƃ��������D
�ƂȂ邱�Ƃ��������D
���̂��߂ɂ́C
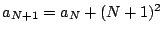 ����
����
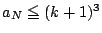 �Ȃ̂�
�Ȃ̂�
�������悢�D
������
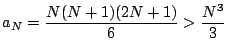 �Ȃ̂�
�Ȃ̂�
�܂�
![$N<\sqrt[3]{3}(k+1)$](images/img966.gif) �D
�D
![$\sqrt[3]{3}<\dfrac{3}{2}$](images/img967.gif) �Ȃ̂�
�Ȃ̂�
(�����F3�J���́@+8 ��+7��)
�� 1.21
���
1.21
-
- (1)
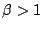 �C
�C 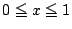 ���
���
��ʂɓ�̎��� 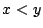 �ɑ���
�ɑ��� ![$[x]\le[y]$](images/img987.gif) �ł��邩��
�ł��邩��
����������
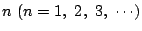 �ɑ���
�ɑ���
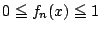 ���������Ώ�̋c�_��
���������Ώ�̋c�_��  �ɑウ��
�ɑウ��
 �ɑ��čs�����Ƃɂ��
�ɑ��čs�����Ƃɂ��
����
���������C 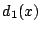 �̌��_�Ƃ��킹�đ�ӂ��������D
�̌��_�Ƃ��킹�đ�ӂ��������D
 �ɑ���
�ɑ���
 �𐔊w�I�A�[�@�Ŏ����D
�𐔊w�I�A�[�@�Ŏ����D
 �̂Ƃ��D
�̂Ƃ��D
![$f_1(x)=\beta x-[\beta x]$](images/img995.gif)
![$f_1(x)=\beta x-[\beta x]$](images/img995.gif) ���
���
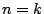 �̂Ƃ�
�̂Ƃ�
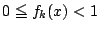 �Ƃ����
�Ƃ����
��蓯�l��
�䂦�ɋA�[�@�ɂ���Ă��ׂĂ�  �ɑ���
�ɑ���
- (2)
- ���w�I�A�[�@�Ŏ����D
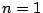 �̂Ƃ��D
�̂Ƃ��D
�ƂȂ�C�����D
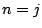 �Ő�������Ƃ���D�܂�
�Ő�������Ƃ���D�܂�
�Ƃ���D���̂Ƃ�
�䂦�� 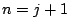 �ł����������D
�ł����������D
���������ċA�[�@�ɂ��
���ׂĂ�
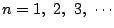 �ɑ���
�ɑ���
�����藧�D
- (3)
- (2)����
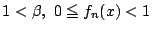 �Ȃ̂�
�Ȃ̂� 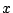 ���Œ肷��Ƃ�
���Œ肷��Ƃ�
����
����͉������Ă���̂��D
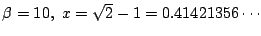 �̂Ƃ��ǂ̂悤�ɂȂ��Ă��邩�D
�̂Ƃ��ǂ̂悤�ɂȂ��Ă��邩�D
����������
�ƂȂ�D
�܂�
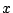
��10�i�W�J���̂��̂ł���D�����
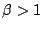
�ł���C�ӂ̎���
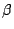
�ɂ��
�W�J�C�����
�i�W�J�Ɋg���������̂ł���D
��
�ʉ��@���R�� �ɑ�
�ɑ�
���������邱�Ƃ𐔊w�I�A�[�@�Ŏ����D
�̂Ƃ��D
�����D
�Ƃ���D���̂Ƃ�

�̂Ƃ��̐��������肵��
�̂Ƃ��̐������������̂ŁC��ʂɐ�������D
��������p���āC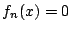 �ƂȂ�
�ƂȂ�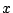 ��
��
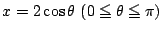 �ƕ\�������̂����߂�D
�ƕ\�������̂����߂�D
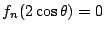 ���
���
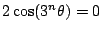 �D�܂�
�D�܂�
�Ƃ�
�͈̔͂łƂ�悢�D���ꂩ��
�܂�
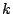
��
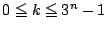
��
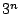
�Ƃ��D
����������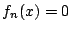 ����
����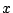 ��
��
��
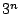
���݂����D���
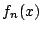
�̎����͖��炩��
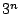
�Ȃ̂ŁC����炪
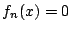
����
�� ���ׂĂł���D����đ�ӂ������ꂽ�D ��
�� 1.23
���
1.23
 �̂Ƃ��D
�̂Ƃ��D 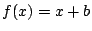 �Ƃ����D
�Ƃ����D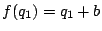 ��
��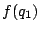 ���L�����Ȃ̂ŁC
���L�����Ȃ̂ŁC 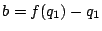 ���L�����ł���D
���L�����ł���D
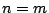 �̂Ƃ���������Ƃ���D
�̂Ƃ���������Ƃ���D
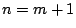 �̂Ƃ��D
�̂Ƃ��D 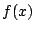 ��
�� 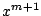 �̌W����1�ł���
�̌W����1�ł��� 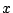 ��
�� 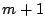 �����Ƃ��C
���قȂ�
�����Ƃ��C
���قȂ� 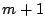 �̗L����
�̗L����
 �ɑ�
�ɑ�
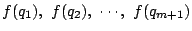 �����ׂėL�����ł���Ƃ���D
�����ׂėL�����ł���Ƃ���D
�����藝���
�ƂȂ�D������
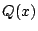
��
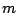
������
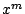
�̌W���͗��ӂ̌W�����r����1�ł���D
 �͂��ׂĈقȂ�̂ŁC
�͂��ׂĈقȂ�̂ŁC
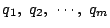 �ɑ�
�ɑ�
����������
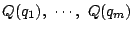
�͂��ׂėL�����ł���D
���w�I�A�[�@�̉��肩�� 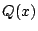 �͗L�����W���̑������ł���D�䂦��
�͗L�����W���̑������ł���D�䂦�� ����
����  ��
�L�����W���̑������ł���D
��
�L�����W���̑������ł���D
���������đ�ӂ������ꂽ�D��
����
���̖��͐��w�I�A�[�@���g�����ƂȂ�������D
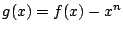 ��
��  �����ł���D
�����ł���D
 �����ׂėL�����ł���D
�����ׂėL�����ł���D
 ����
���� 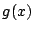 �ɑ���
�ɑ��� ��
��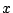 �ɑ���l����܂��
�ɑ���l����܂�� 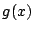 �͈�ӂɒ�܂�D
����
�͈�ӂɒ�܂�D
����
�Ƃ����D���̂Ƃ�
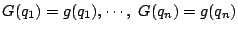
�Ȃ̂ōP�����̌������
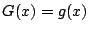
�D
����������
���ꂩ��
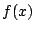
���L�����W����

���������ł��邱�Ƃ������ꂽ�D��
�� ���ꂪ�u���O�����W���̕�Ԍ����v�̕��@�ł���D
��
�� 1.24
���
1.24
��1
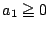 �Ȃ炷�ׂĂ̍������łȂ��a��0�ɂȂ�̂͂��ׂ�0�̂Ƃ��݂̂ɂȂ�D
�䂦��
�Ȃ炷�ׂĂ̍������łȂ��a��0�ɂȂ�̂͂��ׂ�0�̂Ƃ��݂̂ɂȂ�D
�䂦��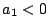 �ł���D���l��
�ł���D���l�� �ł���D����������
�ԍ�
�ł���D����������
�ԍ�
 ��
��
�ƂȂ���̂�����D���̂Ƃ�
�ł��邩��
�i�����F������2�s�ځu>�v���u=�v�Ɂj
�ł���D
��
��2
 ���������Ƃ͓��l�D
���������Ƃ͓��l�D
 �Ɋւ��鐔�w�I�A�[�@�Ŏ����D
���������藧�̂�
�Ɋւ��鐔�w�I�A�[�@�Ŏ����D
���������藧�̂� �ł���D
�ł���D
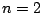 �̂Ƃ��D
�̂Ƃ��D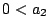 �ł��邩��
�ł��邩��
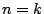
�̂Ƃ����藧�Ƃ���D
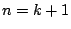
�̂Ƃ��D
��������D
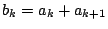
�Ƃ����ƁC
���a��0�ő�������ł���D���w�I�A�[�@�̉��肩��
�ł��邪�C
�Ȃ̂ŁC
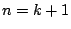
�̂Ƃ������肪��������D
�����
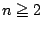
��������D
��
�� 1.25
���
1.25
(1)
����  �̂Ƃ��C�C�ӂ̐��̎���
�̂Ƃ��C�C�ӂ̐��̎���
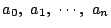 �ɑ���
�ɑ���
�����̉�������������Ƃ𐔊w�I�A�[�@�Ŏ����D
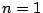 �̂Ƃ��D
�̂Ƃ��D 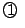 ��
��
�ł��邩��C
�͊m���ɂ�����̐��̉��ł���D
 �̂Ƃ���������Ƃ���D
�̂Ƃ���������Ƃ���D
 �̂Ƃ��D
�̂Ƃ��D
�ƒu���D
�����ŌW��
�͂��ׂĐ��Ȃ̂ŁC
�A�[�@�̉���ɂ����
�͐��̉�����������D
�����  �Ƃ���D
�Ƃ���D
 �Ȃ̂�
�Ȃ̂�  ��
��  �ŕ����琳�ɕς��D
�܂�
�ŕ����琳�ɕς��D
�܂�  ��
�� 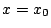 �ŋɏ��ł���D
�ŋɏ��ł���D
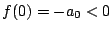 �Ȃ̂�
�Ȃ̂� 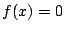 �͂�������̉�
�͂�������̉� 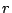 �����D
�����D
(2)
��ʂɕ��f��
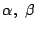 �Ɋւ��ĕs����
�Ɋւ��ĕs����
����������D�䂦��
���������� 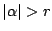 �ł��镡�f��
�ł��镡�f�� 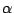 �ɑ��Ă�(1)����
�ɑ��Ă�(1)����
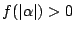 �Ȃ̂�
�Ȃ̂�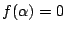 �ƂȂ邱�Ƃ͂��蓾�Ȃ��D
�ƂȂ邱�Ƃ͂��蓾�Ȃ��D
�����1�̑��̉� 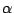 �͂��ׂ�
�͂��ׂ� 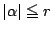 ���݂����D
���݂����D
(3)
�Ƃ����D
���̌W��
�͂��ׂĐ��Ȃ̂ŁC
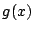
�͎���
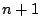
��(1)�̏��������D
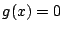 ��
�� 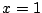 �����ɂ��̂ŁC(2)����
�����ɂ��̂ŁC(2)���� 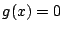 ��
�� 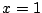 �ȊO��
��
�ȊO��
�� 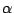 �͂��ׂ�
�͂��ׂ� 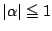 ���݂����D�܂�
���݂����D�܂�
�̉��͂��ׂ�
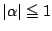
�����D��
����
���� 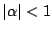 �����藧�D���w�I�A�[�@�̕����ɓI���i�����̂Ŗ���
�����藧�D���w�I�A�[�@�̕����ɓI���i�����̂Ŗ��� 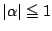 �ɂ��Ă��邪�C���Ђ��̏ؖ����l���Ăق����D
��
�ɂ��Ă��邪�C���Ђ��̏ؖ����l���Ăق����D
��
�� 1.26
���
1.26
-
- (1)
 ���L�����ł���Ƃ���D
���L�����ł���Ƃ���D
�Ƃ����D
���  ��3�̔{���ł���D
��3�̔{���ł���D 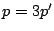 �Ƃ����D
�Ƃ����D
���ꂩ�� 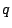 ��3�̔{���ɂȂ�C
��3�̔{���ɂȂ�C
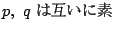 �̉���Ɩ��������D
�̉���Ɩ��������D
����āC 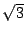 �͗L�����łȂ��D�܂�
�͗L�����łȂ��D�܂� 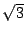 �͖������ł���D
�͖������ł���D
- (2)
- �O�̗L���_
 ��
��
 �����O�p�`�ł�����̂����݂����Ƃ���D
�����O�p�`�ł�����̂����݂����Ƃ���D
���̂Ƃ���̃x�N�g��
�̊e�����͗L�����ł���D
 �̖ʐς��l�����
�̖ʐς��l�����
�܂�
�E�ӂ͗L�����ł��邩�炱��� 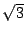 ���������ł��邱�ƂƖ��������D
���������ł��邱�ƂƖ��������D
�����3���_���L���_�ł��鐳�O�p�`�͑��݂��Ȃ��D
�ʉ�
(2)�͎��̂悤�� �Ŏ������Ƃ��ł���D
�Ŏ������Ƃ��ł���D
�ݒ�͓��l�Ƃ���D����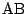 �C����
�C����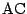 ��
��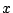 ���̐��̕������Ȃ��p��
���ꂼ��
���̐��̕������Ȃ��p��
���ꂼ��
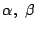 �Ƃ���D�����ꂩ��
�Ƃ���D�����ꂩ�� ���ƕ��s�ȂƂ��́C
�Ӓ����L�����̐��O�p�`�̍����͖������ł��邱�Ƃ���C�������o��D
���ƕ��s�ȂƂ��́C
�Ӓ����L�����̐��O�p�`�̍����͖������ł��邱�Ƃ���C�������o��D
������� ���Ƃ͕��s�łȂ��Ƃ���D
���Ƃ͕��s�łȂ��Ƃ���D
�ł���D
���
���C
�ƂȂ��āC���������L�����̓����ƂȂ薵���ł���D
����đ��݂��Ȃ��D
��
�� 1.27
���
1.27
-
- (1)
- ����
 �̌X����
�̌X����
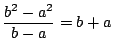 �C���l��
����
�C���l��
����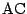 �̌X����
�̌X����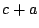 �ł���D�e������
�ł���D�e������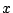 ���̐��̕����ƂȂ��p��
���̐��̕����ƂȂ��p��
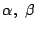 �Ƃ����
�Ƃ����
�ł���D���̂Ƃ�
�ł���D ���������ŁC
���������ŁC
 �͗L�����ł��邩��
�ǂ̂悤��
�͗L�����ł��邩��
�ǂ̂悤�� �ɑ��Ă����ꂪ��v���邱�Ƃ͂Ȃ��D
�܂�
�ɑ��Ă����ꂪ��v���邱�Ƃ͂Ȃ��D
�܂�
 �ƂȂ邱�Ƃ͂Ȃ��D
�ƂȂ邱�Ƃ͂Ȃ��D
- (2)
-
 �Ȃ̂�
�Ȃ̂�
�ł���D �ł��邩��
�ł��邩��
�łȂ���Ȃ�Ȃ��D���ꂩ��
�܂�
�܂�
 �Ȃ̂�
�Ȃ̂�
 �ł���D
�ł���D
��
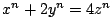 �ɂ��ׂĂ�0�ł͂Ȃ�1�g�̉�
�ɂ��ׂĂ�0�ł͂Ȃ�1�g�̉�
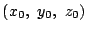 ������Ƃ���D
���̂R���̍ő����
������Ƃ���D
���̂R���̍ő����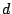 �Ƃ��C
�Ƃ��C
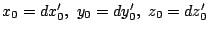 �Ƃ���D
�����
�Ƃ���D
�����
�ł���D����Ă��ׂĂ�0�ł͂Ȃ�1�g�̉�������C
�ő����1�̉�������D
�ő����1��1�g�̉���
 �Ƃ���D
�Ƃ���D
 ���
���  �͋����D
�͋����D  �Ƃ����D���̂Ƃ�
�Ƃ����D���̂Ƃ�
��
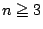
���
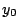
�������D
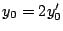
�Ƃ����D���l�ɂ��ꂩ��
��D
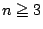
���
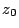
�������D
�Ƃ��낪�����
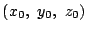 ���ő����1�̉��ł��邱�ƂƖ�������D
���ő����1�̉��ł��邱�ƂƖ�������D
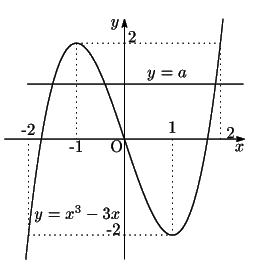
����āC ��3�ȏ�̐����̂Ƃ��C
��3�ȏ�̐����̂Ƃ��C
��������
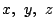
��
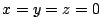
�ȊO�ɑ��݂��Ȃ��D
�ʉ�
���̂悤�ɂ��Ă��悢�D
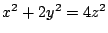 �ɂ��ׂĂ�0�ł͂Ȃ�1�g�̉�
�ɂ��ׂĂ�0�ł͂Ȃ�1�g�̉�
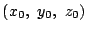 ������Ƃ���D
�`���Ɠ��l�ɂ��āC
������Ƃ���D
�`���Ɠ��l�ɂ��āC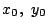 ��2�̔{���ł���D
��2�̔{���ł���D
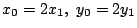 �Ƃ����D
�Ƃ����D
���
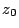
��2�̔{���ł���D
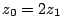
�Ƃ����D���̂Ƃ��Ă�
�ƁC�͂��߂̎��Ɠ������ɂȂ�D
����������
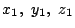
���Ă�3�̔{���ƂȂ�C���̑���͌���Ȃ������邱�Ƃ��ł���D
�܂�
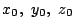 �͂Q�ʼn��x�ł������D
���̂悤�Ȑ���0�ȊO�ɂȂ��D
�͂Q�ʼn��x�ł������D
���̂悤�Ȑ���0�ȊO�ɂȂ��D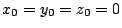 �ƂȂ�D
�ƂȂ�D
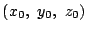 ���u���ׂĂ�0�v�ł͂Ȃ�1�g�̉��ł��������Ƃɔ������D
��
���u���ׂĂ�0�v�ł͂Ȃ�1�g�̉��ł��������Ƃɔ������D
��
�� 1.29
���
1.29
-
- (1)
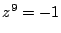 �ł���D�܂�
�ł���D�܂�
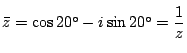 �ł���D
�ł���D
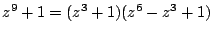 ��
�� 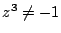 �Ȃ̂�
�Ȃ̂�
�܂� 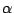 ��
��
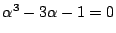 �����̂�
�����̂�
�̉��ł���D
����
�h�E���A�u���̒藝���K���Ă��Ȃ��Ƃ��́C�O�{�p�̌����ł��悢�D
 �ł���D�O�{�p�̌�������
�ł���D�O�{�p�̌�������
���
���ꂩ��
 ���������D
���������D
- (2)
-
 �Ƃ����D
�Ƃ����D
 ���
���  �̉���
�̉��� 
�ł��邩��C  �͈قȂ�3�����������D
�͈قȂ�3�����������D
�L������
 �����Ƃ���D
�����Ƃ���D
���
���ꂩ��
 �Ȃ̂�
�Ȃ̂�  �D������
�D������  �͖��炩�ɉ��łȂ��D
����ėL�����̉��͂Ȃ��D
�͖��炩�ɉ��łȂ��D
����ėL�����̉��͂Ȃ��D
- (3)
 ��������
��������
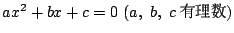 �̉��Ƃ���D
�̉��Ƃ���D
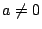 �Ȃ̂�
�Ȃ̂� 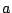 �Ŋ��邱�Ƃɂ��
�Ŋ��邱�Ƃɂ��
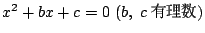 �̉��Ƃł���D
�̉��Ƃł���D
���
�܂�
��1�̏ꍇ 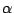 �͗L�����ł��蓾�Ȃ����Ƃɔ�����D
�͗L�����ł��蓾�Ȃ����Ƃɔ�����D
��2�̏ꍇ
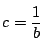 ���
���
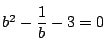 .�܂�
.�܂�
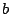 ��
�� 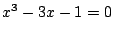 �̉��ł���D�Ƃ��낪
�̉��ł���D�Ƃ��낪 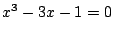 �͗L�����̉���
�������Ȃ��̂ł��邩��C
�͗L�����̉���
�������Ȃ��̂ł��邩��C 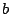 ���L�����ł��邱�ƂƖ��������D
���L�����ł��邱�ƂƖ��������D
����ėL�������W���Ƃ���������ŁC 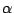 �����Ƃ�����̂͑��݂��Ȃ�
���Ƃ������ꂽ�D
�����Ƃ�����̂͑��݂��Ȃ�
���Ƃ������ꂽ�D
��
�� 1.31
���
1.31
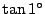 ���L�����ł���Ɖ��肷��D
���L�����ł���Ɖ��肷��D
�܂�
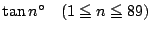 ��
�L�����ƂȂ邱�Ƃ𐔊w�I�A�[�@�Ŏ����D
��
�L�����ƂȂ邱�Ƃ𐔊w�I�A�[�@�Ŏ����D
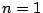 �̂Ƃ��͉��肩��L�����ł���D
�̂Ƃ��͉��肩��L�����ł���D
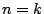 �̂Ƃ��L�����ł���Ƃ���D���̂Ƃ�
�̂Ƃ��L�����ł���Ƃ���D���̂Ƃ�
���
���L�����ł���D
����������
 ���L�����ł���D
���L�����ł���D
����
 �ŁC���ꂪ�L�����ƂȂ����̂�
�ŁC���ꂪ�L�����ƂȂ����̂�
�ƕ����ɕ\�����D���̂Ƃ�
�ł���D
�������̈��������ɂ�����e�f�����̌��͋����Ȃ̂ŁC
���ӂ̈��������ɂ����đf����3�͊����C
�E�ӂ͋�������D
����͖����ł���D
�����
 �͖������ł���D
��
�͖������ł���D
��
�� 1.32
���
1.32
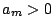 �ł��邱�Ƃ𐔊w�I�A�[�@�Ŏ����D
�ł��邱�Ƃ𐔊w�I�A�[�@�Ŏ����D
��`���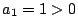 �D
�D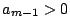 �Ƃ���D
�Ƃ���D 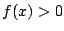 ���
���
�䂦�� 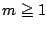 �ɑ���
�ɑ���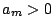 �ł���D���̂Ƃ�
�ł���D���̂Ƃ� 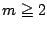 �ɑ���
�ɑ���
 �Ȃ̂�
�Ȃ̂�
�����
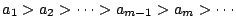 �ƂȂ邱�Ƃ������ꂽ�D
�ƂȂ邱�Ƃ������ꂽ�D
-
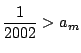 �ƂȂ�
�ƂȂ� 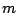 �����݂��Ȃ��Ɖ��肷��D�܂�
�˂�
�����݂��Ȃ��Ɖ��肷��D�܂�
�˂�
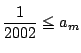 �����藧�Ƃ���D
���ꂩ��
�����藧�Ƃ���D
���ꂩ��
����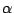 ��
��
 �Ɉ�Ƃ�D
���肩��e
�Ɉ�Ƃ�D
���肩��e �ɑ���
�ɑ��� �ł���D
�ł���D
 �͘A�����ł��邩��
�͘A�����ł��邩��
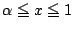 �ɂ�����ő�l�����݂���D
�����
�ɂ�����ő�l�����݂���D
����� 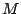 �Ƃ���D
�Ƃ���D 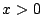 ��
�� 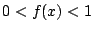 �Ȃ̂�
�Ȃ̂� 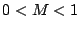 �ł���D
�ł���D
�ł��邪
�Ȃ̂�
���ꂩ��
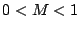 �ł��邩��
�ł��邩��
�����
 ��
�� �Ɩ�������D
����������
�Ɩ�������D
����������
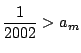 �ƂȂ�
�ƂȂ� 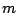 �����݂��邱�Ƃ������ꂽ�D
�����݂��邱�Ƃ������ꂽ�D
��
�� 1.33
���
1.33
�u
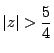 �ƂȂ�ǂ̂悤�ȕ��f��
�ƂȂ�ǂ̂悤�ȕ��f��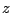 �ɑ��Ă�
�ɑ��Ă�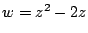 �Ƃ͕\����Ȃ��v
�Ƃ�������̑��
�u
�Ƃ͕\����Ȃ��v
�Ƃ�������̑��
�u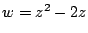 �ƂȂ�
�ƂȂ�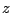 �́C
�́C
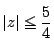 �����v
�ł���D
���̖��肪��������悤��
�����v
�ł���D
���̖��肪��������悤��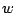 �Ƃ́C�܂�
�Ƃ́C�܂�
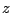 ��2��������
��2��������
��2�����Ƃ���
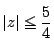
�����悤��
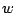
�Ƃ������Ƃł���D
�܂���̏�������2����������(���f)�萔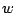 �̏W����
�̏W����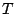 �Ȃ̂ł���D
�Ȃ̂ł���D
���āC
�ЂƂ̕��f��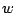 �ɑ���
�ɑ���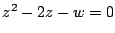 �ƂȂ�
�ƂȂ�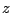 �͓����D
�͓����D
�����
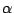
��
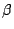
�Ƃ���D���ƌW���̊W����
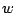 ��
��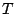 �ɑ����邱�ƂƁC����
�ɑ����邱�ƂƁC����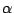 ��
��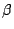 �������
�������
�������Ƃ����l�ł���D
�䂦��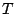 �ɑ�����
�ɑ�����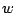 �ɑ��Ă�
�ɑ��Ă�
�����藧�D
�����œ�������������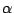 ��
��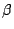 �����݂��邱�Ƃ������D
�����݂��邱�Ƃ������D
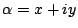 �Ƃ�����
�Ƃ�����
�ӁX������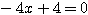 �D�����
�D����� 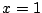 �D
�D
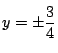 �D�܂�
�D�܂�
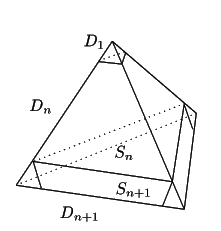
�����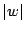 �̍ő�l��
�̍ő�l��
 �ŁC
���̂Ƃ�
�ŁC
���̂Ƃ�
�ł���D
��

 ��: �_�̐��i
�O: �l����
Aozora Gakuen
��: �_�̐��i
�O: �l����
Aozora Gakuen
 �̂Ƃ�
�̂Ƃ�
 �C
�C
 �̂Ƃ���s��(���ׂĂ̐�)�C
�̂Ƃ���s��(���ׂĂ̐�)�C
 �̂Ƃ����Ȃ��D
�̂Ƃ����Ȃ��D
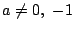 �̂Ƃ�
�̂Ƃ�
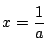 �C
�C
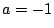 �̂Ƃ���s��(���ׂĂ̐�)�C
�̂Ƃ���s��(���ׂĂ̐�)�C
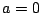 �̂Ƃ����Ȃ��D
�̂Ƃ����Ȃ��D
 �ƂȂ�D�䂦��
�ƂȂ�D�䂦��
 �̂Ƃ�
�̂Ƃ�
 �C
�C
 �̂Ƃ���s��(���ׂĂ̐�)�C
�̂Ƃ���s��(���ׂĂ̐�)�C
 �܂���
�܂���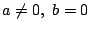 �̂Ƃ����Ȃ��D
�̂Ƃ����Ȃ��D
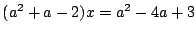 �C
�܂�
�C
�܂�
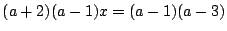 �ƂȂ�D�䂦��
�ƂȂ�D�䂦��
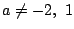 �̂Ƃ�
�̂Ƃ�
 �C
�C
 �̂Ƃ���s��(���ׂĂ̐�)�C
�̂Ƃ���s��(���ׂĂ̐�)�C
 �̂Ƃ����Ȃ��D
�̂Ƃ����Ȃ��D
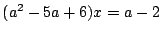 �C
�܂�
�C
�܂�
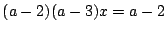 �ƂȂ�D�䂦��
�ƂȂ�D�䂦��
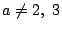 �̂Ƃ�
�̂Ƃ�
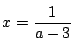 �C
�C
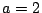 �̂Ƃ���s��(���ׂĂ̐�)�C
�̂Ƃ���s��(���ׂĂ̐�)�C
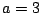 �̂Ƃ����Ȃ��D
�̂Ƃ����Ȃ��D
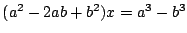 �C
�܂�
�C
�܂�
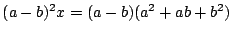 �ƂȂ�D�䂦��
�ƂȂ�D�䂦��
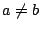 �̂Ƃ�
�̂Ƃ�
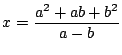 �C
�C
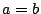 �̂Ƃ���s��(���ׂĂ̐�)�D
�̂Ƃ���s��(���ׂĂ̐�)�D
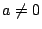 �̂Ƃ�
�̂Ƃ�
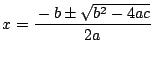 �C
�C
 �̂Ƃ�
�̂Ƃ�
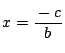 �C
�C
 �̂Ƃ���s��(���ׂĂ̐�)�C
�̂Ƃ���s��(���ׂĂ̐�)�C
 �̂Ƃ����Ȃ��D
�̂Ƃ����Ȃ��D
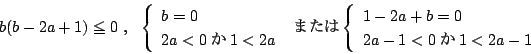
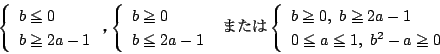 (a2-b �ɒ���)
(a2-b �ɒ���)
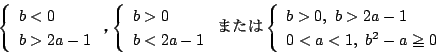 (a2-b �ɒ���)
(a2-b �ɒ���) ��̏�������
��̏������� 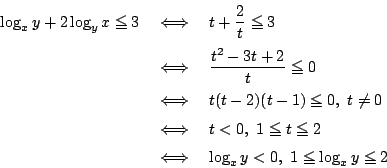 �@�@(�C�͂܂��͂ł���)
�@�@(�C�͂܂��͂ł���)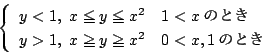 �@(0<x1�ɒ���)
�@(0<x1�ɒ���)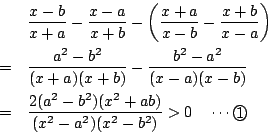
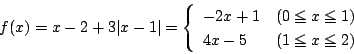
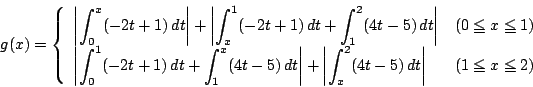
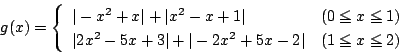
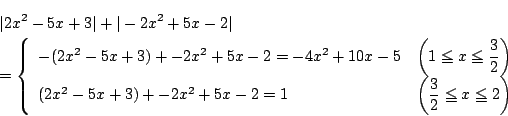
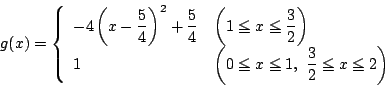

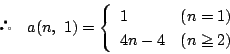

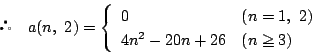

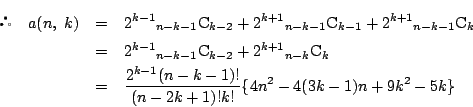
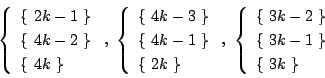
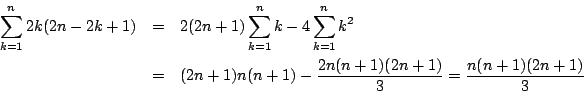
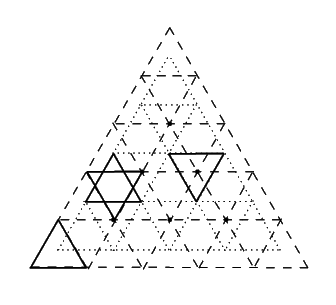
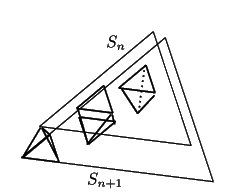 �}�̂悤��3��ނ̗��̂��m�F�����D
�}�̂悤��3��ނ̗��̂��m�F�����D
 �����
�����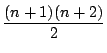 �D
�D
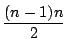 �D
�D
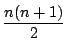 �D
�D
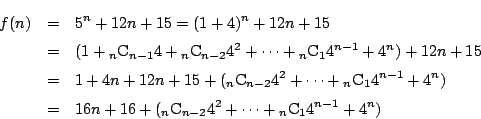

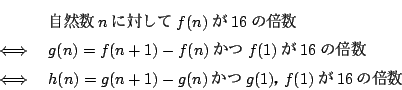
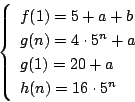
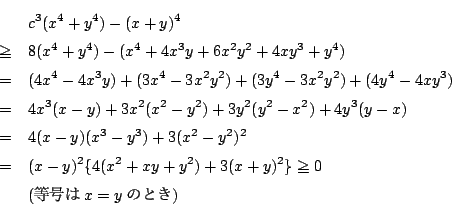
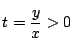 �Ƃ����D
�Ƃ����D
![$t=\dfrac{1}{\sqrt[3]{c^3}-1}>0$](images/img813.gif) �ŋɏ����ŏ��D
�ŋɏ����ŏ��D
![\begin{eqnarray*}
&&f \left( \dfrac{1}{\sqrt[3]{c^3}-1}\right) \ge 0\\
&\iff& c...
...qrt[3]{c^3}-1\\
&\iff& \sqrt[3]{c^3}-1 \ge 1\\
&\iff& c^3\ge 8
\end{eqnarray*}](images/img814.gif)
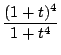 �̍ő�l�ȏ�͈̔͂ł���D
�̍ő�l�ȏ�͈̔͂ł���D
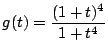 �Ƃ���D
�Ƃ���D
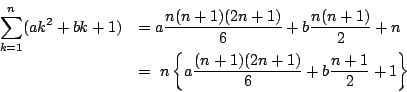
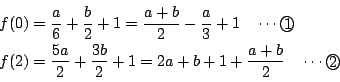
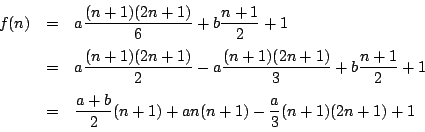
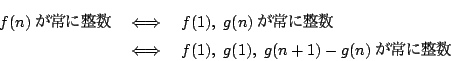
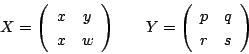
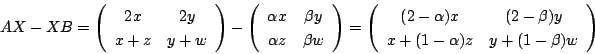
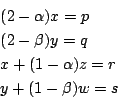
 �D
�D
 �̂Ƃ��C
�̂Ƃ��C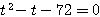
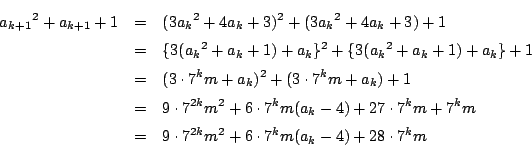
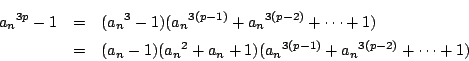
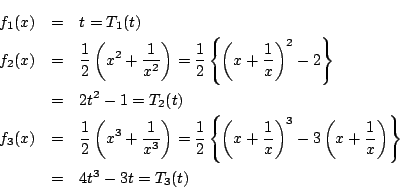
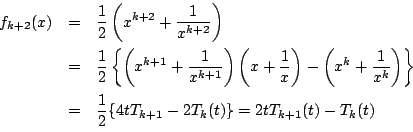
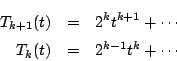
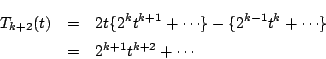
![\begin{eqnarray*}
T_{k+2}(\cos \theta)&=&2\cos \theta T_{k+1}(\cos \theta)-T_k(\...
...os\{(k+2)\theta\} + \cos k \theta]-\cos k \theta=\cos(k+2)\theta
\end{eqnarray*}](images/img928.gif)
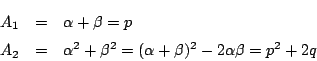
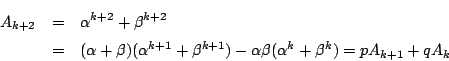
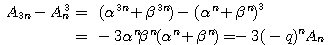
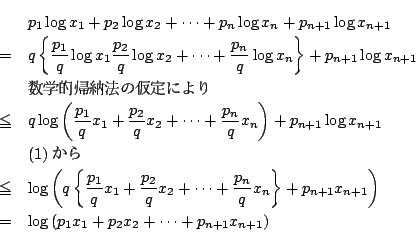
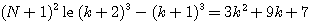
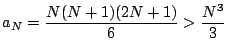 �Ȃ̂�
�Ȃ̂�
![$\sqrt[3]{3}<\dfrac{3}{2}$](images/img967.gif) �Ȃ̂�
�Ȃ̂�
![\begin{eqnarray*}
��&&3k^2+9k+8-(N+1)^2\\
&\ge&3k^2+9k+8- \left(\sqrt[3]{3}k+...
...�\quad 9-5\sqrt[3]{3}=729^{\frac{1}{3}}
-375^{\frac{1}{3}}>0 )
\end{eqnarray*}](images/img969.gif)
![$\dfrac{5}{4}<\sqrt[3]{3}$](images/img979.gif) �Ȃ̂�
�Ȃ̂�
![\begin{eqnarray*}
��&&2N^2+10N+13-(3k^2+9k+7)\\
&>&2 \left(\sqrt[3]{3}k-\dfra...
...3^{\frac{2}{3}}-3)k^2+(7\cdot3^{\frac{1}{3}}-9)k
-\dfrac{3}{8}
\end{eqnarray*}](images/img981.gif)
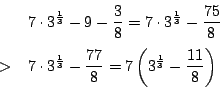
![\begin{eqnarray*}
&&\beta^1x-\sum_{k=1}^1\beta^{1-k}d_k(x)\\
&=&\beta x-d_1(x)\\
&=&\beta x-[\beta x]=f_1(x)
\end{eqnarray*}](images/img1003.gif)
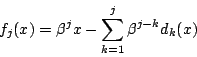
![\begin{eqnarray*}
f_{j+1}(x)&=&f(f_j(x))=\beta f_j(x)-[\beta f_j(x)]\\
&=&\be...
...j+1}(x)\\
&=&\beta^{j+1}x-\sum_{k=1}^{j+1}\beta^{j+1-k}d_k(x)
\end{eqnarray*}](images/img1005.gif)
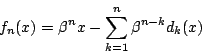
![\begin{displaymath}
\begin{array}{ll}
d_1(x)=[10x]=4&f_1(x)=10x-[10x]=0.142135...
...10f_3(x)-[10f_3(x)]=0.1356\cdots\\
\cdots&\cdots
\end{array}\end{displaymath}](images/img1010.gif)
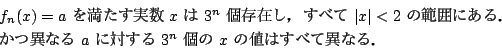
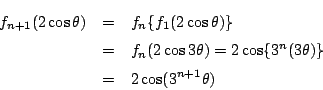
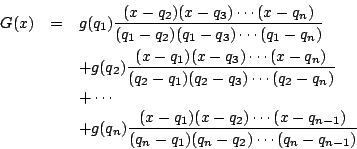
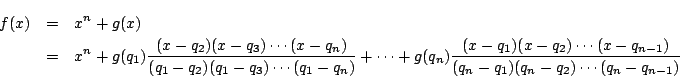
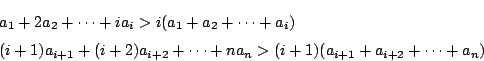
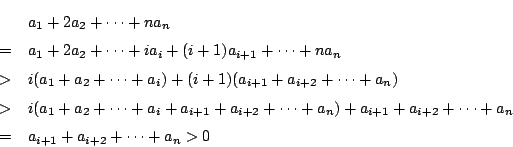
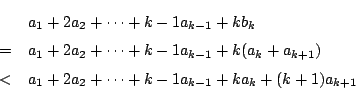
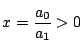 �͊m���ɂ�����̐��̉��ł���D
�͊m���ɂ�����̐��̉��ł���D

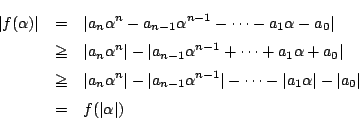
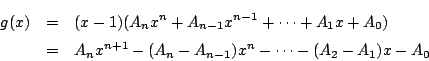
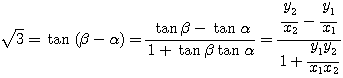
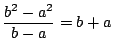 �C���l��
����
�C���l��
����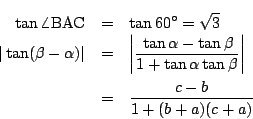
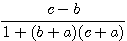 �͗L�����ł��邩��
�ǂ̂悤��
�͗L�����ł��邩��
�ǂ̂悤�� �ł���D
�ł���D
 �����Ƃ���D
�����Ƃ���D
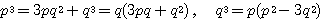
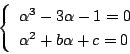
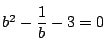 .�܂�
.�܂�
 �Ƃ����D
�Ƃ����D
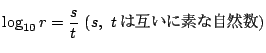 �Ƃ����D
�Ƃ����D
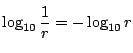 ��
�L�����ł���D
��
�L�����ł���D
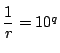 �ƕ\����D
�ƕ\����D
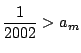 �ƂȂ�
�ƂȂ� 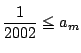 �����藧�Ƃ���D
���ꂩ��
�����藧�Ƃ���D
���ꂩ��
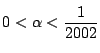 �Ɉ�Ƃ�D
���肩��e
�Ɉ�Ƃ�D
���肩��e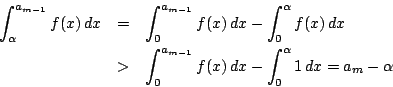
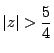 �ƂȂ�ǂ̂悤�ȕ��f��
�ƂȂ�ǂ̂悤�ȕ��f��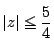 �����v
�ł���D
���̖��肪��������悤��
�����v
�ł���D
���̖��肪��������悤��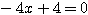 �D�����
�D����� 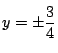 �D�܂�
�D�܂�