次の各問いに答えよ.
- (1)
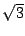 は無理数であることを示せ.
は無理数であることを示せ.
- (2)
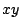 平面上の点
平面上の点 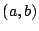 は,
は, 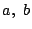 がともに有理数のときに
有理点と呼ばれる.
がともに有理数のときに
有理点と呼ばれる. 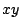 平面において,三つの頂点がすべて有理点である
正三角形は存在しないことを示せ.
平面において,三つの頂点がすべて有理点である
正三角形は存在しないことを示せ.
次の各問いに答えよ.
![]() は整数で,
は整数で,![]() をみたす.放物線
をみたす.放物線![]() 上に3点
上に3点
![]() ,
,
![]() ,
,
![]() をとる.
をとる.
複素数
![]() と,それに共役な複素数
と,それに共役な複素数 ![]() に対し
に対し
![]() とする.
とする.
![]() を実数全体で定義された連続関数で,
を実数全体で定義された連続関数で, ![]() で
で ![]() を満たすものとする.
を満たすものとする.
![]() とし,順に,
とし,順に,
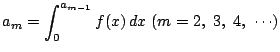 により
数列
により
数列 ![]() を定める.
を定める.
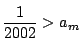 となる
となる