

 次: 3章解答
上: 問題と考え方
前: 問題
次: 3章解答
上: 問題と考え方
前: 問題
1.26
[99阪大改題]
問題
1.26
解答
1.26
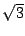 を用いることがヒントになっている.
するとこれは面積か傾きで矛盾を作るのではないかと考えられる.
これらを2通りの方法で表してみよう.
を用いることがヒントになっている.
するとこれは面積か傾きで矛盾を作るのではないかと考えられる.
これらを2通りの方法で表してみよう.
1.27
[04一橋前期]
問題
1.27
解答
1.27
前問別解と同様に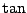 の加法定理が使える.
(2)は必要条件から絞って調べよう.
の加法定理が使える.
(2)は必要条件から絞って調べよう.
1.28
[00千葉]
問題
1.28
解答
1.28
これは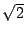 は無理数であることと同様の方法で示せる.
ただ,有理数の場合既約分数にとれることは証明なしに使ったが,
この場合はそれに対応する準備が必要だ.3数の最大公約数が1であるようにとれるかを考えよう.
は無理数であることと同様の方法で示せる.
ただ,有理数の場合既約分数にとれることは証明なしに使ったが,
この場合はそれに対応する準備が必要だ.3数の最大公約数が1であるようにとれるかを考えよう.
1.29
[00九州大改題]
問題
1.29
解答
1.29
(2)と(3)が背理法である.
(2):整数係数で最高次数の係数が1の方程式が有理数解をもてばその解は整数である,
まずこれを示して背理法の論証を進める.
(3):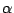 が3次方程式,かつ2次方程式の解であるとすると,
3次式を2次式で割った余りの1次式でできる方程式の解になる!
ここに気づいたら,ていねいに論証を進めよう.
が3次方程式,かつ2次方程式の解であるとすると,
3次式を2次式で割った余りの1次式でできる方程式の解になる!
ここに気づいたら,ていねいに論証を進めよう.
1.30
[98一橋]
問題
1.30
解答
1.30
(1),(3)が背理法である.(2)の「限る」とは必要条件であることを示せということである.
数学特有の言い方にも慣れていこう.
1.31
[06京大後期文系5番理系6番]
問題
1.31
解答
1.31
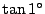 が有理数なら
が有理数なら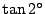 も有理数?
順にいけば
も有理数?
順にいけば
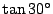 も有理数となる.
背理法と帰納法を結合させればよいと見通せる.
も有理数となる.
背理法と帰納法を結合させればよいと見通せる.
1.32
[02名大前期理系]
問題
1.32
解答
1.32
存在しないということは? すべての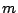 に対し
に対し
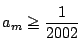 ということだ.
一方(1)をうまく用いて,
ということだ.
一方(1)をうまく用いて,
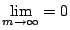 を示せば矛盾である.
を示せば矛盾である.
1.33
[05東大理科改題]
問題
1.33
解答
1.33
条件自体を対偶でいいかえてみよう.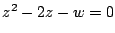 の解がすべて
の解がすべて
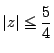 にあるということだ.
これがわかれば
にあるということだ.
これがわかれば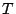 を具体的に求めなくても本問は解ける.
を具体的に求めなくても本問は解ける.
Aozora Gakuen
![]() を用いることがヒントになっている.
するとこれは面積か傾きで矛盾を作るのではないかと考えられる.
これらを2通りの方法で表してみよう.
を用いることがヒントになっている.
するとこれは面積か傾きで矛盾を作るのではないかと考えられる.
これらを2通りの方法で表してみよう.![]() は無理数であることと同様の方法で示せる.
ただ,有理数の場合既約分数にとれることは証明なしに使ったが,
この場合はそれに対応する準備が必要だ.3数の最大公約数が1であるようにとれるかを考えよう.
は無理数であることと同様の方法で示せる.
ただ,有理数の場合既約分数にとれることは証明なしに使ったが,
この場合はそれに対応する準備が必要だ.3数の最大公約数が1であるようにとれるかを考えよう.![]() が3次方程式,かつ2次方程式の解であるとすると,
3次式を2次式で割った余りの1次式でできる方程式の解になる!
ここに気づいたら,ていねいに論証を進めよう.
が3次方程式,かつ2次方程式の解であるとすると,
3次式を2次式で割った余りの1次式でできる方程式の解になる!
ここに気づいたら,ていねいに論証を進めよう.