

 次: 帰納的定義
上: 問題と考え方
前: 問題
次: 帰納的定義
上: 問題と考え方
前: 問題
1.2
問題
1.2
解答
1.2
係数比較法と代入法の両方が考えられる.
代入法では少しの工夫が必要である.つまり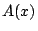 の形を推測して,
その形が次数より多い
の形を推測して,
その形が次数より多い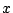 の値で成り立つことを示すのである.
の値で成り立つことを示すのである.
1.3
問題
1.3
解答
1.3
まず次数を決定する.最高次の項が両辺一致することで次数は決まる.
この最高次の項を除く部分が恒等式になるように,適当な代入によって係数を決めていく.
1.4
問題
1.4
解答
1.4
定点を通ることは,すべての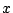 と
と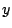 で成立するということである.
これをいかすと,交点を実際に求めなくても交点を通る直線を決定できる.
で成立するということである.
これをいかすと,交点を実際に求めなくても交点を通る直線を決定できる.
1.5
問題
1.5
解答
1.5
(2)は(1)の一般化である.
(1)から余りの形を推測する.
余りの次数は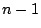 次以下であるが,
余りの形が
次以下であるが,
余りの形が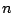 個の異なる
個の異なる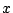 で成立すれば,それは恒等式である.
で成立すれば,それは恒等式である.
1.6
問題
1.6
解答
1.6
二つ以上の対称軸をもつものは三角関数である.
この対称軸を二つ選び,それが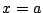 と
と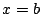 となるように拡大と移動すればよい.
これで(1)が得られる.
(2)は二つの対称性を用いて,無数の
となるように拡大と移動すればよい.
これで(1)が得られる.
(2)は二つの対称性を用いて,無数の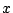 の値で同じ値をとることを示せばよい.
の値で同じ値をとることを示せばよい.
1.7
考え方
1.7
解答
1.7
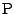 が変化しても変化しない不動の関係式を見つけたい.
この場合は体積である.長さの比を体積の比に置きかえ,逆数の和をとると一定であることがわかる.
が変化しても変化しない不動の関係式を見つけたい.
この場合は体積である.長さの比を体積の比に置きかえ,逆数の和をとると一定であることがわかる.
1.8
問題
1.8
解答
1.8
これは意外に難問である.力ずくの計算では大変だ.
しかし示すべき式は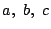 で対称である.
ということは,大小を仮定してもよいということだ.
で対称である.
ということは,大小を仮定してもよいということだ.
1.9
問題
1.9
解答
1.9
正三角形を角度でとらえるか,辺の長さでとらえるか.
いずれかの方針を決めて,条件を書き出す.そのとき,対称性に注意して計算をきれいに進めよう.
Aozora Gakuen
![]() を
を![]() で割った式の余りを文字に置いて除法の等式を立てる.
その上でその式の
で割った式の余りを文字に置いて除法の等式を立てる.
その上でその式の![]() に
に![]() を代入する.または両辺微分する.
(1)をこの方法で確認してから
を代入する.または両辺微分する.
(1)をこの方法で確認してから![]() を一般的に置き(1)を用いて係数を決定する.
を一般的に置き(1)を用いて係数を決定する.![]() を
を![]() で割った式の余りを文字に置いて除法の等式を立てる.
その上でその式の
で割った式の余りを文字に置いて除法の等式を立てる.
その上でその式の![]() に
に![]() を代入する.または両辺微分する.
(1)をこの方法で確認してから
を代入する.または両辺微分する.
(1)をこの方法で確認してから![]() を一般的に置き(1)を用いて係数を決定する.
を一般的に置き(1)を用いて係数を決定する.![]() と
と![]() となるように拡大と移動すればよい.
これで(1)が得られる.
(2)は二つの対称性を用いて,無数の
となるように拡大と移動すればよい.
これで(1)が得られる.
(2)は二つの対称性を用いて,無数の![]() の値で同じ値をとることを示せばよい.
の値で同じ値をとることを示せばよい.