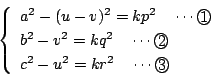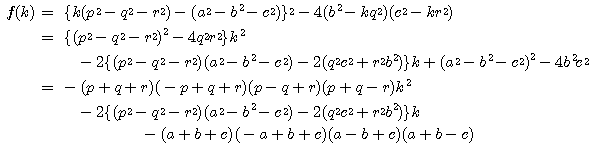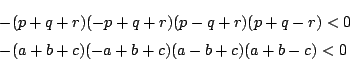-
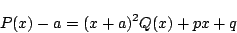
とおく.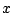 に
に 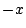 を代入する.
を代入する.
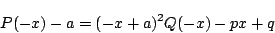
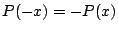 より両辺を
より両辺を 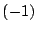 で割って
で割って
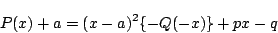
第二の条件から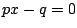 .ゆえに
.ゆえに 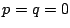 .
したがって
.
したがって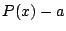 は
は  で割り切れることが示された.
で割り切れることが示された.
-
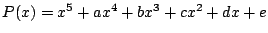 とおく.第一の条件から
とおく.第一の条件から
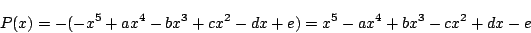
ゆえに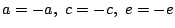 よりこれらは0.このとき
よりこれらは0.このとき
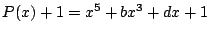 .
これを
.
これを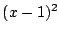 で割ると余りは
で割ると余りは
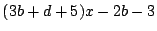 .
.
この余りが0なので,
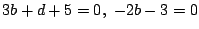 より
より
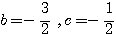 .
.
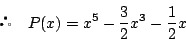
この余りが0なので,
![]() より
より
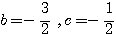 .
.
次に![]() の両辺を
の両辺を ![]() で微分して
で微分して
あわせて
注意
![]() とおく.このとき
とおく.このとき
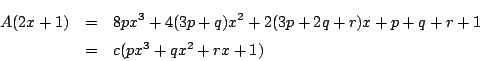
係数を比較して
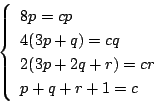
別解
![]() であり,条件式の最高次の項の係数比較から
であり,条件式の最高次の項の係数比較から![]() である.
である.
![]() を代入して
を代入して![]() .これから
.これから![]() .
同様に
.
同様に
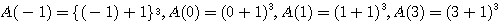
![]() が定数なら
が定数なら ![]() であるがこれは題意をみたさない.
であるがこれは題意をみたさない.
![]() を
を ![]() 次式とし,
次式とし,
![]() とおく.
とおく.
![\begin{eqnarray*}
&&(x+1)f(x+1)-xf(x)\\
&=&(x+1)^{n+1}+a_{n-1}(x+1)^n+\cdots+...
...[n-1次以下の項]\\
&&f(x+2)+2f(x-1)\\
&=&3x^n+[n-1次以下の項]
\end{eqnarray*}](images/img822.gif)
![]() とおく.条件式に
とおく.条件式に ![]() を代入すると
を代入すると
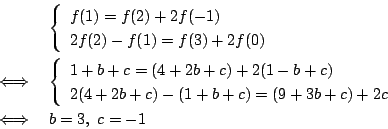
問題の条件式は両辺二次式であるが,二次の項が一致するように次数を定めたので,
それを除くと一次式である.したがって![]() の下では,
の下では,
![]() で条件式が成立すれば恒等的に成立する.
つまり
で条件式が成立すれば恒等的に成立する.
つまり![]() は十分条件である.
は十分条件である.
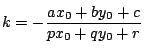 である.
これから求める直線の式は
である.
これから求める直線の式は
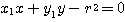
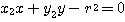
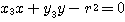
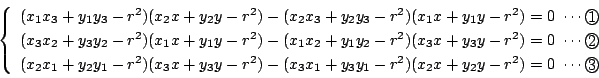
![]() を
を ![]() で割った余りが
で割った余りが ![]() なので
なので
つまり ![]() が
が
![]() について成り立つ.
について成り立つ.
これは左辺が ![]() 次の整式
次の整式 ![]() について
について![]() が,
が,
![]() 個の異なる
個の異なる ![]() の値
の値
![]() で成立することを
示している.
で成立することを
示している.
ゆえにこれは恒等式である.つまり求める余りは ![]() である.
である.
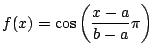 とする.
とする.
![]() は
は
![]() で定義され,
で定義され,
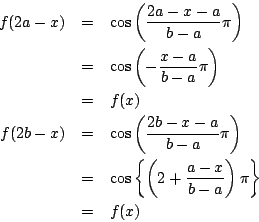
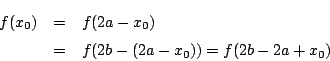
![]() が整式であるから,
が整式であるから,![]() は恒等式である.つまり
は恒等式である.つまり![]() は定数である.
は定数である.
![]() で四面体
で四面体![]() の体積を表す.
の体積を表す.
四面体![]() と四面体
と四面体![]() は,
ともに底面が
は,
ともに底面が
![]() であり,
頂点
であり,
頂点![]() からと頂点
からと頂点![]() から底面への
から底面への![]() 垂線の足の
長さの比は
垂線の足の
長さの比は
![]() に等しい.
に等しい.
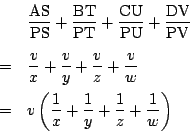
四面体![]() は4つの四面体
は4つの四面体
![]() ,
,
![]() ,
,
![]() ,
,
![]() に分割されるので
に分割されるので
ここで相加相乗平均の関係より
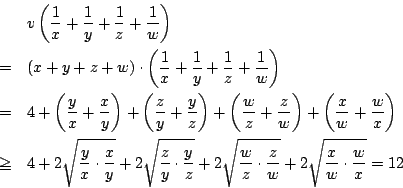
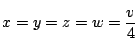 のとき.
のとき.
これを実現する点![]() は適当な基準点
は適当な基準点![]() によって次式で定まる点である.
によって次式で定まる点である.
実際このとき
最小値は12 で最小値を与える点Pは![]() で定まる点(四面体
で定まる点(四面体![]() の重心)である.
の重心)である.
□
示すべき式は![]() で対称である.ゆえに
で対称である.ゆえに![]() として一般性を失わない.
として一般性を失わない.
この場合,三角形の成立条件は![]() である.つまり
である.つまり
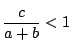 .
また,
.
また,
一方
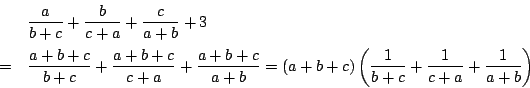
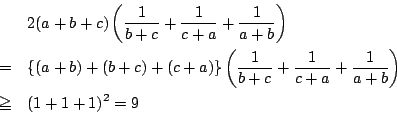
したがって
等号成立は![]() のとき.
のとき.
別解
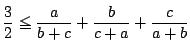 は次のように
力ずくでもできる.
は次のように
力ずくでもできる.
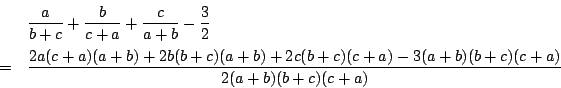
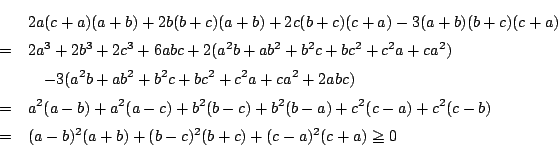
【解法1】
(1)
辺 PQ の傾きは
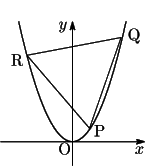 である. PQ が
である. PQ が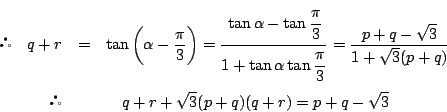
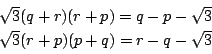
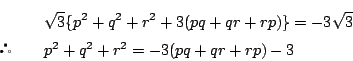
【解法2】
(1)
正三角形の1辺を![]() とする.
とする.
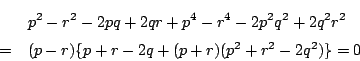
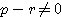 なので
なので
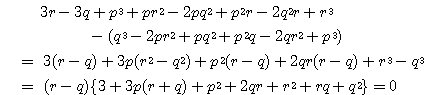
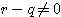 なので
なので
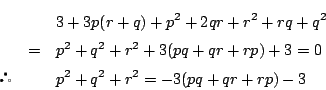
条件は![]() と
と![]() に関して対称である.
に関して対称である.
これを![]() と
と![]() の連立1次方程式として解く.
の連立1次方程式として解く.
![]() ,および
,および
![]() から
から
![]() と
と![]() は2次方程式
は2次方程式
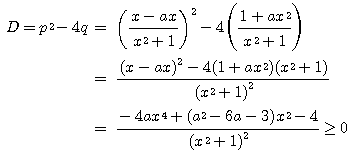
![]() と
と![]() で実数となるものが存在するためには
で実数となるものが存在するためには![]() を満たす実数
を満たす実数![]() が存在すればよい.
が存在すればよい.
これは![]() に関する2次不等式である.
に関する2次不等式である.![]() とおき
とおき
![]() なので,
なので,![]() は条件を満たす.
は条件を満たす.
![]() のときは,
のときは,![]() .
.![]() ではつねに
ではつねに![]() なので条件を満たさない.
なので条件を満たさない.
![]() のとき.軸
のとき.軸![]() .判別式
.判別式![]() が条件である.これから
が条件である.これから
したがって実数![]() が存在するための実数
が存在するための実数![]() の条件は
の条件は
解1
![]() 両編成で隣り合った車両の少なくとも一方が赤色となるような色の塗り方が
両編成で隣り合った車両の少なくとも一方が赤色となるような色の塗り方が![]() 通りあるとする.
そのうち,
通りあるとする.
そのうち,
![]() 番目の列車が赤色である塗り方が
番目の列車が赤色である塗り方が![]() 通り,
通り,
![]() 番目の列車が青色である塗り方が
番目の列車が青色である塗り方が![]() 通り,
通り,
![]() 番目の列車が黄色である塗り方が
番目の列車が黄色である塗り方が![]() 通りとする.
通りとする.
![]() 番目の列車を赤色にできるために
番目の列車を赤色にできるために![]() 番目の列車の色はいずれでもよく,
番目の列車の色はいずれでもよく,
![]() 番目の列車を青色か黄色にできるために
番目の列車を青色か黄色にできるために![]() 番目の列車は赤色でなければならない.
番目の列車は赤色でなければならない.
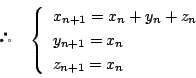
これから
![]() は
は
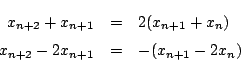
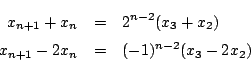
![]() なので,
なので,
解2
![]() 両編成で隣り合った車両の少なくとも一方が赤色となるような色の塗り方が
両編成で隣り合った車両の少なくとも一方が赤色となるような色の塗り方が![]() 通りあるとする.
通りあるとする.
![]() 両編成の場合の色の塗り方を次のように場合に分ける,
両編成の場合の色の塗り方を次のように場合に分ける,
これらの総計が![]() である.
ゆえに
である.
ゆえに
(以下,漸化式を解くのは解1と同じ.) □
第![]() 世代に
世代に![]() 個となるのは,
個となるのは,
![]() 世代に
世代に![]() 個で,そのうちの
個で,そのうちの![]() 個が2個に分裂する場合である.
ここで
個が2個に分裂する場合である.
ここで![]() より
より
![$0\le r\le \left[\dfrac{m}{2} \right]$](images/img958.gif) の範囲である.ただし,実数
の範囲である.ただし,実数![]() に対して
に対して![]() は
は![]() を超えない最大の整数を表す.
したがって次の漸化式が成り立つ.
を超えない最大の整数を表す.
したがって次の漸化式が成り立つ.
![\begin{displaymath}
P_{n+1}(m)=\sum_{r=0}^{\left[\frac{m}{2}\right]}
{}_{m-r} \mathrm{C}_r(1-p)^rp^{m-2r}P_n(m-r)
\quad \cdots\maru{1}
\end{displaymath}](images/img960.gif)
![]() のとき.
のとき.![]() の和は
の和は![]() だけだから次式となる.
だけだから次式となる.
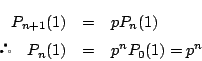
![]() のとき.
のとき.![]() の和は
の和は![]() をわたるから
をわたるから
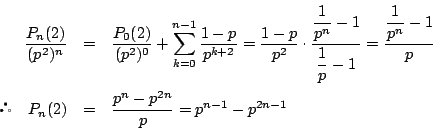
![]() のとき.
のとき.![]() の和は
の和は![]() をわたるから
をわたるから

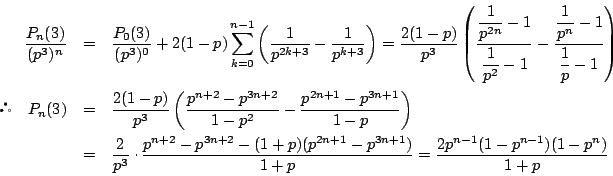
□
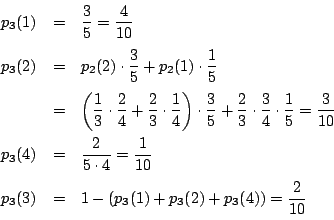
訂正:p3(1)=2/5=4/10 に.
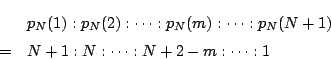
![]() のときは(1)で確認したように成立している.
したがって
のときは(1)で確認したように成立している.
したがって![]() のときは成立している.
のときは成立している.
![]() のとき
のとき![]() の範囲の
の範囲の![]() で成立しているとする.
で成立しているとする.
![]() のとき,
のとき,![]() で示せばよい.
で示せばよい.
![]() と帰納法の仮定から
と帰納法の仮定から
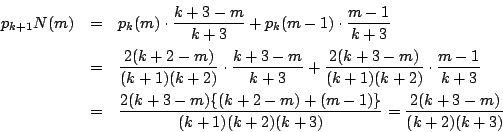
訂正:pk+1N(m) を pk+1(m) に.
![]() 回目に赤玉が出る確率を
回目に赤玉が出る確率を![]() とおく.
とおく.
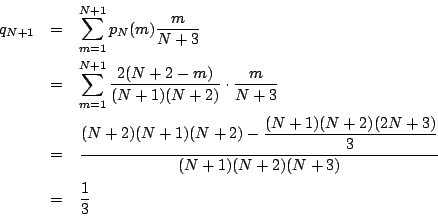
別解
![]() を次のように直接計算してもよい.
を次のように直接計算してもよい.
それぞれの玉を区別する.
![]() 回の試行で玉の選び方の総数は
回の試行で玉の選び方の総数は
赤をどこで選ぶかが
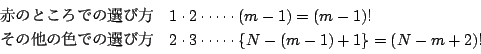
![]() のとき,
のとき,
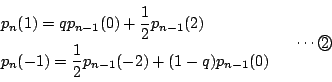
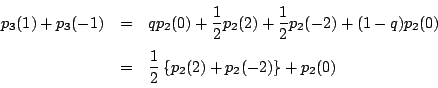
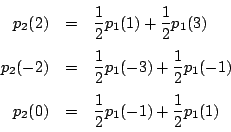
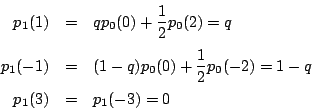
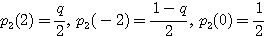
![]() とおく.
とおく.
![]() であり,
であり,![]() なら
なら
![]() である.
である.
![]() のとき.
のとき.
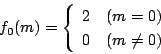
![]() のとき成立するとする.
のとき成立するとする.
![]() より
より![]() なら
なら
また![]() のときは
のときは![]() より
より
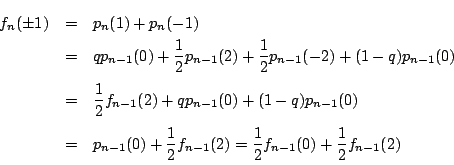
数学的帰納法の仮定から
![]() は
は![]() によらないので,
によらないので,
![]() のときも
のときも![]() によらないことが示された.
によらないことが示された.
よって![]() に対してつねに命題が成立することが示された.
に対してつねに命題が成立することが示された.
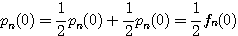
![]() 秒後に0であるのは,1秒間に
秒後に0であるのは,1秒間に![]() 変化する場合と
変化する場合と![]() 変化する場合とが同数であるとき,
そしてそのときにかぎる.
変化する場合とが同数であるとき,
そしてそのときにかぎる.
ゆえに![]() が奇数なら
が奇数なら![]() .
.
![]() が偶数なら
が偶数なら![]() の変化と
の変化と![]() の変化が
の変化が![]() 回ずつ起こればいいので
回ずつ起こればいいので
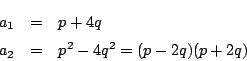
![]() なので
なので![]() と
と![]() に公約数があれば,それは
に公約数があれば,それは![]() の約数でもある.
それが2なら
の約数でもある.
それが2なら![]() が偶数となり結果
が偶数となり結果![]() が偶数.よって
が偶数.よって![]() .これは
.これは![]() と矛盾.
ゆえに
と矛盾.
ゆえに![]() と
と![]() の公約数は
の公約数は![]() と
と![]() の公約数から得られる.ところが
の公約数から得られる.ところが
ゆえに![]() と
と![]() が1より大きい公約数
が1より大きい公約数![]() をもつならば,それは
をもつならば,それは![]() である.
である.
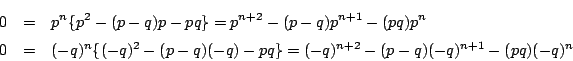
第1式-4×第2式より
そのためには(1)から![]() と
と![]() が3の倍数でなければならない.
が3の倍数でなければならない.
![]() から
から![]() .これを満たす
.これを満たす![]() で積
で積![]() が最小のものは,まず
が最小のものは,まず![]() を最小に取り
を最小に取り![]() .
.
![]() の3の倍数で最小は
の3の倍数で最小は![]() .ゆえに
.ゆえに ![]() が求めるものである.
が求めるものである.
ところが ![]() と
と ![]() の偶数,奇数は一致する.
ゆえに
の偶数,奇数は一致する.
ゆえに ![]() と
と ![]() は偶数,奇数が逆になり,積
は偶数,奇数が逆になり,積![]() はつねに
偶数,つまり
はつねに
偶数,つまり ![]() は8の倍数.
は8の倍数.
ゆえに求める必要十分条件は ![]() が8の倍数であることである.
が8の倍数であることである.
注意 後半の十分性の証明が典型的な「妖怪をつれてくる」方式,つまり作ってみせる方式である. □
![]() とおく.
とおく.

したがって各共通集合は
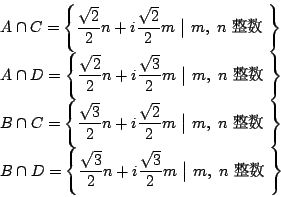
中点が ![]() の要素になっているためには,その2点がともにこの四つの共通集合のなかの同じ集合
の要素であって,しかも実部と虚部の
の要素になっているためには,その2点がともにこの四つの共通集合のなかの同じ集合
の要素であって,しかも実部と虚部の ![]() と
と ![]() がそれぞれともに偶数か,ともに奇数かのときである.
がそれぞれともに偶数か,ともに奇数かのときである.
この違いは合計16通りである.したがって,17個の複素数よりなる集合![]() の中には.
四つの共通集合のなかの同じ集合に属し,しかも実部と虚部の
の中には.
四つの共通集合のなかの同じ集合に属し,しかも実部と虚部の ![]() と
と ![]() の偶数奇数がそれぞれ同じである二つの要素がある.
の偶数奇数がそれぞれ同じである二つの要素がある.
この2点の中点は再び ![]() の要素になっている.
□
の要素になっている.
□
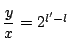 となり整数である.
となり整数である.
ここで ![]() とおく.
とおく.![]() は
は ![]() より小さい平方数なので,
より小さい平方数なので,
![]() .
ゆえに
.
ゆえに
![]() より
より ![]() . つまり
. つまり ![]() であるが,偶数奇数を考え
であるが,偶数奇数を考え
![]() ,つまり
,つまり ![]() .
.
したがって
![]() となる.つまり
となる.つまり
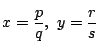 があるとする.
ここで各分数は既約であるとする.
があるとする.
ここで各分数は既約であるとする.
したがって,
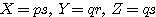 をもつことを示している.
をもつことを示している.
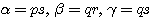
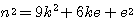 であるから,
であるから,
よって,②の左辺も3の倍数になるのは,
![]() がともに
3の倍数のときにかぎる.
がともに
3の倍数のときにかぎる.
![]() とおき②に代入して,
両辺を3で約すると,
とおき②に代入して,
両辺を3で約すると, ![]() が3の倍数になる.
が3の倍数になる.
つまり![]() も3の倍数となり,
も3の倍数となり,
![]() が互いに素なことに矛盾した.
が互いに素なことに矛盾した.
よって, 有理数解は存在しない.
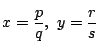 があるとする.ここで各分数は既約であるとする.
があるとする.ここで各分数は既約であるとする.
したがって,
③から, ![]() が9の倍数になるので,
が9の倍数になるので, ![]() も3の倍数.
も3の倍数.
![]() のいずれの組合せでも,このようになる場合,もとの分数の既約性と矛盾する.
のいずれの組合せでも,このようになる場合,もとの分数の既約性と矛盾する.
別解
有理数解
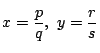 があるとする. 代入し分母を払うと,
があるとする. 代入し分母を払うと,
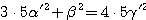
順列の ![]() 番目までにある白の個数を
番目までにある白の個数を![]() ,黒の個数を
,黒の個数を ![]() とする.
とする.
左端が黒の場合,その黒石が条件を満たす(全て取り除かれる).
左端は白とする.
このとき ![]() 番目におかれているのは黒石である.
なぜならそれが白なら
番目におかれているのは黒石である.
なぜならそれが白なら
また ![]() 番目が黒石のとき
番目が黒石のとき
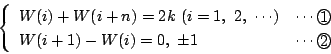
![]() なら,
なら,
![]() 番と
番と![]() 番のあいだ,
および
番のあいだ,
および![]() 番と
番と![]() 番のあいだの2箇所でひもを切って
番のあいだの2箇所でひもを切って![]() 個ずつの2組に分ければ,
どちらの組も白玉
個ずつの2組に分ければ,
どちらの組も白玉![]() 個,黒玉
個,黒玉![]() 個からなる.
よって
個からなる.
よって![]() となる番号
となる番号![]() が存在することを示せばよい.
が存在することを示せばよい.
もし![]() なら
なら![]() が条件を満たす.
が条件を満たす.
![]() とする.
とする.![]() から
から
![]() のときも同様である.
□
のときも同様である.
□
この選手は,平均すれば1kmを3分間で走っている.
40km のコースの![]() km から
km から![]() km の間を
km の間を![]() 分で走るとする.
選手の走る速さは位置および時間に対し連続的に変化するので,
分で走るとする.
選手の走る速さは位置および時間に対し連続的に変化するので,![]() は
は![]() の連続関数である.
の連続関数である.
![]() なら区間0kmから1km の区間が条件を満たす.
なら区間0kmから1km の区間が条件を満たす.
![]() とする.もし
とする.もし
![]() のいずれもが3以下ならば,
のいずれもが3以下ならば,
ゆえに
![]() のうち少なくとも一つは3より大きい.
それを
のうち少なくとも一つは3より大きい.
それを![]() とする.
すると
とする.
すると
![]() の場合も同様である.
□
の場合も同様である.
□
はじめ ![]() を図1のように
を図1のように
![]() と垂直であるようにおく.
このとき
と垂直であるようにおく.
このとき
![]() が鋭角三角形なので,
点
が鋭角三角形なので,
点 ![]() は線分
は線分 ![]() 上にある.
上にある.
![]() を図2のように
を図2のように
![]() が線分
が線分 ![]() に
関して同じ側にあるように連続的に動かす.
に
関して同じ側にあるように連続的に動かす.
そして図3のように
![]() と
と ![]() が垂直であるところまで
動かす.同様にして
が垂直であるところまで
動かす.同様にして
![]() を連続的に変化させると,
を連続的に変化させると,
![]() とのなす角も連続して変化する.
とのなす角も連続して変化する.
したがって中間値の定理によって ![]() が図の範囲を動くとき
途中で
が図の範囲を動くとき
途中で
また辺 AB と辺 CD が垂直ではないので
![]() である.したがって四点 A,B,
である.したがって四点 A,B,
![]() はすべて異なっている.
はすべて異なっている.
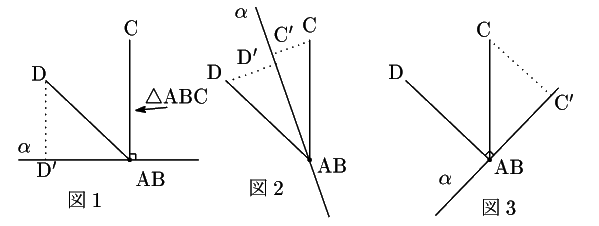
別解
![]() を動かす範囲をもう少し狹めてもできる.
を動かす範囲をもう少し狹めてもできる.
![]() を
を
![]() が
が ![]() 上にあるところから
上にあるところから
![]() が
が ![]() 上にあるようになるまで,上と同じく
上にあるようになるまで,上と同じく
![]() が線分
が線分 ![]() に
関して同じ側にあるように連続的に動かす.
に
関して同じ側にあるように連続的に動かす.
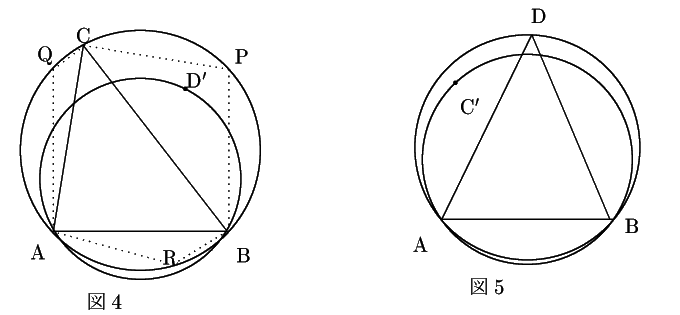
![]() が
が ![]() 上にあるとき,
上にあるとき, ![]() はどこにあるか.
はどこにあるか.
ここで,
![]() の外接円をかき,
の外接円をかき,
![]() の各頂点からその頂点を共有する辺に垂直な直線を引くと,
それらは2本ずつ外接円周上で交わる.例えば
の各頂点からその頂点を共有する辺に垂直な直線を引くと,
それらは2本ずつ外接円周上で交わる.例えば ![]() と
と![]() について,
について,
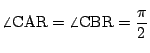 なので,
なので,
![]() となり,四点
となり,四点
![]() は同一円周上にあるからである.他も同様.
は同一円周上にあるからである.他も同様.
![]() は六角形
は六角形
![]() の内部にあり,
したがって
の内部にあり,
したがって
![]() の外接円の内部にある.
の外接円の内部にある.
円弧 ![]() は
は
![]() の外接円の内部に含まれる.
の外接円の内部に含まれる.
![]() が
が ![]() 上にあるようになったときは,
逆に円弧
上にあるようになったときは,
逆に円弧 ![]() が
が
![]() の外接円の内部に含まれる.
の外接円の内部に含まれる.
![]() の動きに対して二つの円は連続的に変化するから,途中で二つの円が一致するときがある.
の動きに対して二つの円は連続的に変化するから,途中で二つの円が一致するときがある.
つまり,四点が同一円周上にあるときが存在する. □
![]() と
と
![]() の3辺をそれぞれ
の3辺をそれぞれ
![]() と
と![]() とする.三角形の成立条件から
とする.三角形の成立条件から
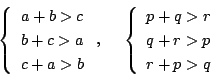
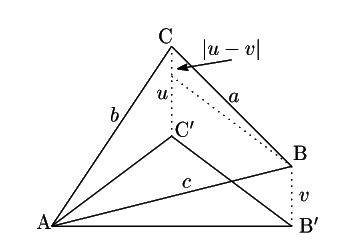 平行移動して点
平行移動して点