![]() は
は ![]() の5次式で,次の2条件:
の5次式で,次の2条件:
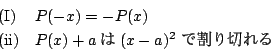
(I)を(i)に訂正.
次の各問いに答えよ.
![]() は実数の定数とする.
は実数の定数とする.
![]() で定義された関数
で定義された関数 ![]() は次の
[
は次の
[ ![]() ],[
],[ ![]() ]を満たすとする.
]を満たすとする.
[ ![]() ]
] ![]() のグラフは,直線
のグラフは,直線 ![]() に関して対称である.
に関して対称である.
[ ![]() ]
] ![]() のグラフは,直線
のグラフは,直線 ![]() に関して対称である.
に関して対称である.
このとき,
四面体![]() の内部の点Pを取る.
直線APと
の内部の点Pを取る.
直線APと
![]() の交点をS,
直線BPと
の交点をS,
直線BPと
![]() の交点をT,
直線CPと
の交点をT,
直線CPと
![]() の交点をU,
直線DPと
の交点をU,
直線DPと
![]() の交点をVとする.
このとき
の交点をVとする.
このとき
放物線![]() 上の相異なる3点 P,Q,R は
上の相異なる3点 P,Q,R は
![]() が正三角形になるように動いている.
が正三角形になるように動いている.