先頭車両から順に1から![]() まで番号のついた
まで番号のついた![]() 両編成の列車がある.
ただし,
両編成の列車がある.
ただし,![]() とする.各車両を赤色,青色,黄色のいずれか1色で塗るとき,
隣り合った車両の少なくとも一方が赤色となるような色の塗り方は何通りか.
とする.各車両を赤色,青色,黄色のいずれか1色で塗るとき,
隣り合った車両の少なくとも一方が赤色となるような色の塗り方は何通りか.
先頭車両から順に1から![]() まで番号のついた
まで番号のついた![]() 両編成の列車がある.
ただし,
両編成の列車がある.
ただし,![]() とする.各車両を赤色,青色,黄色のいずれか1色で塗るとき,
隣り合った車両の少なくとも一方が赤色となるような色の塗り方は何通りか.
とする.各車両を赤色,青色,黄色のいずれか1色で塗るとき,
隣り合った車両の少なくとも一方が赤色となるような色の塗り方は何通りか.
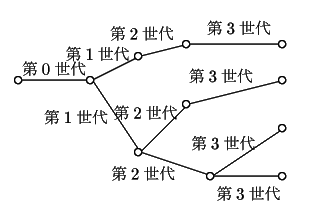 各世代ごとに,各個体が,他の個体とは独立に,
確率
各世代ごとに,各個体が,他の個体とは独立に,
確率![]() で1個,確率
で1個,確率![]() で2個の新しい個体を次の世代に残し,
それ自身は消滅する細胞がある.ただし
で2個の新しい個体を次の世代に残し,
それ自身は消滅する細胞がある.ただし![]() とする.
とする.
いま,第0世代に1個であった細胞が,第![]() 世代に
世代に![]() 個となる確率を,
個となる確率を,
![]() と書くことにしよう.
と書くことにしよう.
![]() を自然数とするとき,
を自然数とするとき,![]() ,
,![]() ,
,![]() を求めよ.
を求めよ.
袋の中に赤と黄と青の玉が1個ずつ入っている.「この袋から玉を1個取り出して戻し,出た玉と同じ色の玉を袋の中に1個追加する」という操作を![]() 回繰り返した後,赤の玉が袋の中に
回繰り返した後,赤の玉が袋の中に![]() 個ある確率を
個ある確率を![]() とする.
とする.
整数に値をとる変数![]() の値が,以下の規則で変化する.
の値が,以下の規則で変化する.
![]() から始めて,
から始めて,![]() 秒後
秒後
![]() に
に![]() である確率を
である確率を![]() とする.
とする.
素数![]() に対して
に対して
![]() を自然数とする.
を自然数とする.![]() 平面上で
平面上で![]() 座標も
座標も![]() 座標も整数である点全体の集合を
座標も整数である点全体の集合を![]() で表す.今点
で表す.今点![]() 上に球を1個置き,次の操作
上に球を1個置き,次の操作![]() を
を![]() 回繰り返し行うことにより球を
回繰り返し行うことにより球を![]() 上で動かす.
上で動かす.
操作![]() を1回行った時点で球が置かれている点の座標を
を1回行った時点で球が置かれている点の座標を![]() で表す.
同様に,操作
で表す.
同様に,操作![]() を
を
![]() 繰り返し行った時点で
球が置かれている点の座標を
繰り返し行った時点で
球が置かれている点の座標を![]() で表す.
で表す.![]() の部分集合
の部分集合
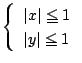 の表す領域を
の表す領域を