![]() は
は ![]() または正の整数とする.方程式
または正の整数とする.方程式 ![]() の解
の解
![]() で
で ![]() がともに奇数であるものを奇数解とよぶ.
がともに奇数であるものを奇数解とよぶ.
- (1)
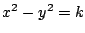 が奇数解をもてば,
が奇数解をもてば,
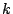 は
は 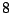 の倍数であることを示せ.
の倍数であることを示せ.
- (2)
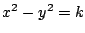 が奇数解をもつための必要十分条件を求めよ.
が奇数解をもつための必要十分条件を求めよ.
![]() は
は ![]() または正の整数とする.方程式
または正の整数とする.方程式 ![]() の解
の解
![]() で
で ![]() がともに奇数であるものを奇数解とよぶ.
がともに奇数であるものを奇数解とよぶ.
0以上の整数 ![]() に対して,
に対して, ![]() で
で ![]() の下2桁を表すことにする.
たとえば,
の下2桁を表すことにする.
たとえば,
![]() である.
である. ![]() を2でも5でも割り切れない正の整数とする.
を2でも5でも割り切れない正の整数とする.
複素数平面において集合
![]() を次のように定義する.
を次のように定義する.
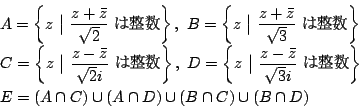
![]() を100以下の自然数の集合とする.
また,50以下の自然数
を100以下の自然数の集合とする.
また,50以下の自然数![]() に対し,
に対し,
![]() の要素でその奇数の約数のうち最大のものが
の要素でその奇数の約数のうち最大のものが![]() となるものからなる集合を
となるものからなる集合を![]() とする.
このとき,次の問いに答えよ.
とする.
このとき,次の問いに答えよ.
自然数 ![]() と
と ![]() 項数列
項数列
![]() が与えられていて,
次の条件(
が与えられていて,
次の条件(
![]() )を満たしている.
)を満たしている.
(i) ![]() はすべて正整数で,すべて1と
はすべて正整数で,すべて1と ![]() の間にある.
の間にある.
![]()
(ii)
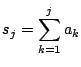 とおくとき,
とおくとき,
![]() はすべて平方数である.
(整数の2乗である数を平方数という.)
はすべて平方数である.
(整数の2乗である数を平方数という.)
白石180個と黒石181個の合わせて361個の碁石が横に一列に並んでいる.碁石が どのように並んでいても,次の条件を満たす黒の碁石が少なくとも一つあることを示せ.
その黒の碁石とそれより右にある碁石をすべて除くと,残りは白石と黒石が同 数となる.ただし,碁石が一つも残らない場合も同数とみなす.
![]() は自然数で
は自然数で![]() とする.
穴のあいた
とする.
穴のあいた![]() 個の白玉と
個の白玉と![]() 個の黒玉にひもを通して輪を作る.
このとき適当な2箇所でひもを切って
個の黒玉にひもを通して輪を作る.
このとき適当な2箇所でひもを切って![]() 個ずつの2組に分け,
どちらの組も白玉
個ずつの2組に分け,
どちらの組も白玉![]() 個,黒玉
個,黒玉![]() 個からなるようにできることを
示せ.
個からなるようにできることを
示せ.
あるマラソン選手は出発地点から40kmの地点までちょうど2時間で走った. このとき,途中のある3分間でちょうど1kmの距離を進んだことを説明せよ.
各面が鋭角三角形からなる四面体 ABCD において 辺 AB と辺 CD は垂直で
はないとする.このとき辺 AB を含む平面 ![]() に点 C,点 D から下ろした垂線の
足をそれぞれ
に点 C,点 D から下ろした垂線の
足をそれぞれ
![]() とするとき,4点 A,B,
とするとき,4点 A,B,
![]() がすべて相異なり,しかも同一円周上にあるように
がすべて相異なり,しかも同一円周上にあるように ![]() がとれることを示せ.
がとれることを示せ.
平面![]() に対し,
に対し,
![]() の各頂点
の各頂点
![]() を通り
平面
を通り
平面![]() に垂直な直線の
に垂直な直線の![]() との交点をそれぞれ
との交点をそれぞれ
![]() とする.
このようにして得られた
とする.
このようにして得られた
![]() を
を
![]() の平面
の平面![]() への正射影という.
への正射影という.
任意の2つの三角形
![]() と
と
![]() に対し,次の条件を満たす平面
に対し,次の条件を満たす平面![]() が存在することを示せ.
が存在することを示せ.