次の三つの等号はそれぞれ意味が異なる.
このように等号はいろんな意味があるので,
常に意識して等号の意味を考えなければならない.
そこで,恒等式を特徴づける基本性質を示そう.
定理 1
![]() が高々
が高々![]() 次の
次の ![]() についての整式であるとき,
次の三つの命題は同値である.
またこのとき,等式
についての整式であるとき,
次の三つの命題は同値である.
またこのとき,等式 ![]() は 恒等式 であるという.
は 恒等式 であるという.
証明
ゆえに三つの条件は互いに他の二つの必要十分条件になっていることが示された. □
これをおさえて次の例題を考えよう. 問題を読んだら少し自分で考えてみてほしい.
例題 1.1 [法政大過去問]
![]() を三次以下の整式とする.恒等的に
を三次以下の整式とする.恒等的に
![]() が成立すれば,
任意の
が成立すれば,
任意の ![]() に対しても恒等的に
に対しても恒等的に
![]() が成立することを示せ.
が成立することを示せ.
考え方
この問題を普通は次のように![]() の整式の問題として解く.
しかしまた
の整式の問題として解く.
しかしまた![]() に関する整式と見ることもできる.
に関する整式と見ることもできる.
解答1
![]() とおく.
とおく.
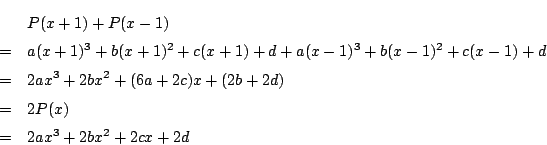
ここで少し観点を変え,![]() の式と見てみよう.
の式と見てみよう.
解答2
これが「恒等式を発見する」ということである. 大切なことは「どの文字について恒等式か」を考えることだ. もう一つ例題をしよう.
例題 1.2 [早稲田過去問改題]
直線 ![]() は
は ![]() がどんな値をとっても, ある一定の
がどんな値をとっても, ある一定の![]() 軸と平行な軸をもつ
放物線と接している.この放物線の方程式を求めよ.
軸と平行な軸をもつ
放物線と接している.この放物線の方程式を求めよ.
考え方 これにも実は2通りの方法がある.直線と連立するとつねに重解をもつような2次関数を求めればよい. 一方直線の通過領域を求めてもよいのだ.直線は通過領域の境界の曲線と接しながら動いていく.
解答
求める放物線を
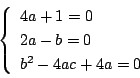
これには別解がある.前節の「図形は点の集合だ」を参考にしてほしい.
別解
直線 ![]() の通過範囲を求める.
の通過範囲を求める.
注意 図形的には通過領域の境界にもとの直線が接するのは当然だが, 念のためそれを確認した.
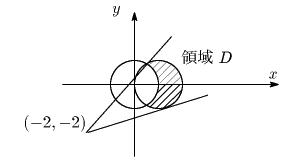
不等式
![]() で定まる領域を
で定まる領域を ![]() とする.
とする. ![]() が
この領域を動くとき,
が
この領域を動くとき,
![]() の最大値と最小値を求めよ.
の最大値と最小値を求めよ.
 解答
解答
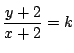 とおく.
とおく.
したがって,点 ![]() と,領域
と,領域 ![]() 内の点を結ぶ直線の
傾きの最大値と最小値を求めればよい.
二円の交点は
内の点を結ぶ直線の
傾きの最大値と最小値を求めればよい.
二円の交点は
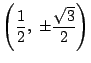 で
これらを通るときの傾きは,
で
これらを通るときの傾きは,
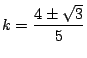 .
また円
.
また円 ![]() と接する傾きは直線と点
と接する傾きは直線と点 ![]() との距離が1になるときなので,
との距離が1になるときなので,
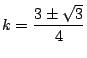 .
これらを比較し図を考えて
.
これらを比較し図を考えて
このように関数の値域を図から考えるときに, 不動点があれば考察は明快になる.