ただし次の二点に注意しよう.
第一に曲線![]() は交点を通る曲線をすべて表すわけではない.
第二に曲線
は交点を通る曲線をすべて表すわけではない.
第二に曲線![]() は
は ![]() 自身は表せない.
自身は表せない.
例
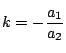 なら1次式になるので直線,
その他の場合は放物線を表す.
なら1次式になるので直線,
その他の場合は放物線を表す.
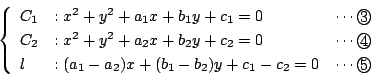
円![]() と直線
と直線![]() の交点を通りかつ原点も通る円の方程式を求めよ.
の交点を通りかつ原点も通る円の方程式を求めよ.
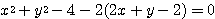 ⇔
⇔ 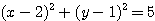
円と円,円と直線の交点を通る円はいつもこのように
元の二式と係数![]() などを用いて書けるのだろうか.
それを考えるのが次の例題である.
などを用いて書けるのだろうか.
それを考えるのが次の例題である.
二つの円![]() が次の方程式で与えられている.
が次の方程式で与えられている.
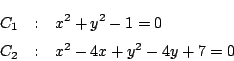
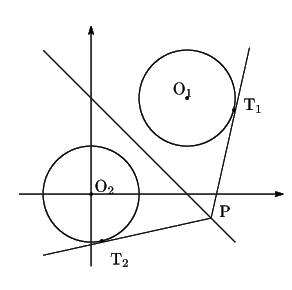 (1) 2円の中心をそれぞれ
(1) 2円の中心をそれぞれ
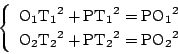
(2)
![]() を変形する.
を変形する. ![]() なら直線なので,
なら直線なので, ![]() とする.
とする.
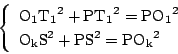
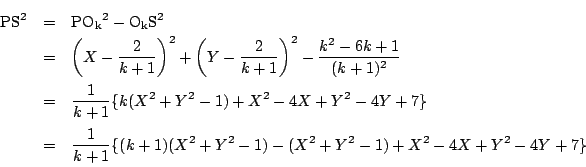
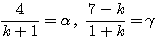
となればよいが,これを![]() で表すと
で表すと
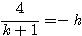 …①
…① 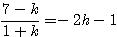 …②
…②
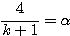 より
より
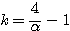 とおけばよい.
この
とおけばよい.
この