二変数の基本対称式は, 2次方程式の解と係数の関係に現れる.
つまり, 2次方程式 ![]() の解を
の解を
![]() とするとき
とするとき
三変数の場合 ![]() の
の ![]() をどのように入れ替えても式がかわらない
場合に対称式という.三変数の基本対称式は
をどのように入れ替えても式がかわらない
場合に対称式という.三変数の基本対称式は
一般に,
![]() の
の ![]() 変数の多項式は
変数の多項式は ![]() 個の基本対称式をもつ.
個の基本対称式をもつ.
この証明は青空学園のなかにある『不変式』を見てほしい.ここではこれに関する過去問題をやってみよう.
例題 1.8 [95年上智大]
![]() を2変数
を2変数 ![]() に関する実数を係数にもつ多項式とする.
に関する実数を係数にもつ多項式とする.
![]() とおく. このとき, 以下の問いに答えよ.
とおく. このとき, 以下の問いに答えよ.
1.
(i)
![]() のとき
のとき ![]() を
を ![]() と
と ![]() を用いて表せ.
を用いて表せ.
(ii) 一般に ![]() は
は ![]() と
と ![]() との多項式で表されることを示せ.
との多項式で表されることを示せ.
(iii) 恒等的に
![]() が成り立つならば
が成り立つならば ![]() は
は ![]() と
と ![]() との多項式であることを示せ.
との多項式であることを示せ.
(iv) 恒等的に
![]() が成り立つならば
が成り立つならば ![]() は
は ![]() と
と ![]() との多項式であることを示せ.
との多項式であることを示せ.
2.
(i) 恒等的に
![]() が成り立つならば
が成り立つならば
![]() が成り立つことを示せ.
が成り立つことを示せ.
(ii) 上の性質をもつ多項式はどのようなものか.
解答
1.
(i) ![]() を
を ![]() を用いて表すと
を用いて表すと
![]()
よって
![]()
(ii)
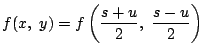 より,
より, ![]() は
は
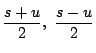 の多項式となるから
の多項式となるから ![]() と
と ![]() との多項式で表される.
との多項式で表される.
(iii)
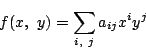
とおく.
![]() が恒等的に成り立つとき
が恒等的に成り立つとき
![]()
よって![]() が奇数のときは
が奇数のときは![]() である.
つまり
である.
つまり![]() は
は ![]() の多項式,
つまり
の多項式,
つまり ![]() と
と ![]() の多項式となる.
の多項式となる.
(iv) (iii)と同様において考えると
![]() が恒等的に成り立つとき
が恒等的に成り立つとき
![]()
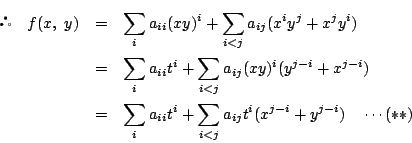
0と自然数![]() に対して
に対して
![]() が
が![]() と
と![]() の多項式になることを,
次数
の多項式になることを,
次数![]() についての数学的帰納法で示す.
についての数学的帰納法で示す.
![]() であるので
であるので![]() で成立.
で成立.
![]() が
が ![]() の多項式であると仮定する.
の多項式であると仮定する.
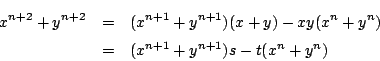
より
![]() も
も ![]() の多項式となる.
よって
の多項式となる.
よって![]() は
は ![]() の多項式となる.
の多項式となる.
したがって, ![]() により
により ![]() は
は ![]() の多項式となる.
の多項式となる.
別解
![]() の各単項式の
の各単項式の ![]() の次数と
の次数と ![]() の次数の和をその単項式の次数とよび, その中で最大のものを
の次数の和をその単項式の次数とよび, その中で最大のものを ![]() の次数とよぶ.
の次数とよぶ.
![]() が成り立つような
が成り立つような ![]() の次数
の次数 ![]() についての帰納法で示す.
についての帰納法で示す.
![]() のときは明らかに成立する.
のときは明らかに成立する.
![]() で成立するとし,
で成立するとし, ![]() を
を ![]() 次対称式とする.
次対称式とする.
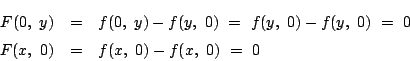
2.
(i)
![]() が恒等的に成り立つとき
が恒等的に成り立つとき
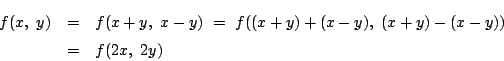
(ii) (1)の(iii)と同様において考えると,
![]() が恒等的に成り立つとき
が恒等的に成り立つとき
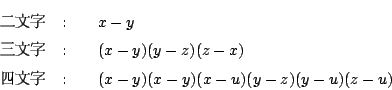
四文字の第2項(x-z)に訂正.
いろんな計算で, 差積をくくることで見通しがよくなることが多い. これから出てくるたびに注意する. 式が出てくれば, 対称式か交代式かをまずみるようにしよう.
求めるべき三数![]() に関する条件が対称なら,
に関する条件が対称なら,![]() を満たすもので求めて,それからそれらを相互に入れ替えたものが,すべて求めるものになる.
を満たすもので求めて,それからそれらを相互に入れ替えたものが,すべて求めるものになる.
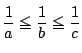 なので
なので
考え方 式の対称性と交代性をいかして,式の因子を見出すのである. 大文字のものは適当な置きかえで,最初の小文字の等式が活用できるようにする.
解答
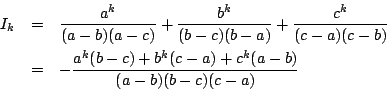
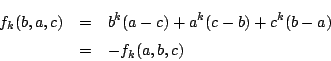
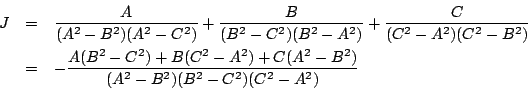
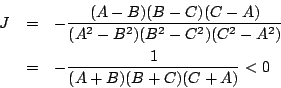
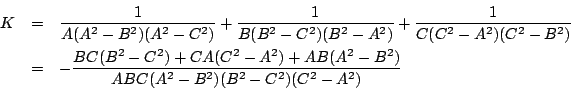
例題 1.11 [89京大文系]
五つの実数
![]() があり,どの
があり,どの![]() も他の四つの相加平均
より大きくはないという.このような
も他の四つの相加平均
より大きくはないという.このような
![]() をすべて求めよ.
をすべて求めよ.
考え方
5文字
![]() について条件は対称だ.この対称性をどのように活かすか.
方法はいくつかある.一つで終わりにせずいろいろ考えてみよう.
について条件は対称だ.この対称性をどのように活かすか.
方法はいくつかある.一つで終わりにせずいろいろ考えてみよう.
解法1
条件は
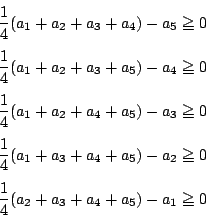
各辺を加えると
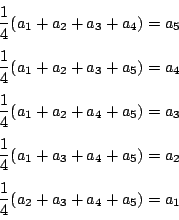
解法2
条件は5文字
![]() について対称である.
したがって
について対称である.
したがって
逆にすべて等しければ条件をみたすことは明らか.
□