容器 A には 3% の食塩水が 300g ,容器 B には 6% の食塩水が
300g 入れてある.A,B からそれぞれ 100g の食塩水をとってAの分をBに,
B の分をAに入れる.このような操作を ![]() 回
回
![]() 繰り返して行った後の,容器 A の食塩水の濃度を求めよ.
繰り返して行った後の,容器 A の食塩水の濃度を求めよ.
容器 A には 3% の食塩水が 300g ,容器 B には 6% の食塩水が
300g 入れてある.A,B からそれぞれ 100g の食塩水をとってAの分をBに,
B の分をAに入れる.このような操作を ![]() 回
回
![]() 繰り返して行った後の,容器 A の食塩水の濃度を求めよ.
繰り返して行った後の,容器 A の食塩水の濃度を求めよ.
考え方 濃度の違う食塩水を交互に入れていくので,もちろん濃度は1回ごとの操作で変化していく. しかし,このような操作で変わらないものがある.そう.二つの容器に入っている塩の量の和 は一定だ.
解答
![]() 回の操作の後で 容器 A の食塩水の濃度が
回の操作の後で 容器 A の食塩水の濃度が ![]() ,
容器 B の食塩水の濃度が
,
容器 B の食塩水の濃度が ![]() であるとする.
すると,操作後の塩が操作前のどこから来たかを考えることで次の連立漸化式が得られる.
であるとする.
すると,操作後の塩が操作前のどこから来たかを考えることで次の連立漸化式が得られる.
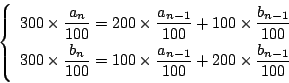
つぎに変化する量のなかで,変化しない関係を見いだす例題を考えよう.
![]() が与えられている.
が与えられている.
![]() を
を
![]() の内部の点とし,
の内部の点とし,
![]() を点
を点 ![]() から辺
から辺
![]() に下ろした垂線の足とする.
このとき
に下ろした垂線の足とする.
このとき
解答
頂点
![]() の対辺を
の対辺を ![]() ,
線分
,
線分
![]() の
長さを
の
長さを ![]() とする.
とする.
![]() はちょうど
はちょうど
![]() の面積である.
よって
の面積である.
よって
ここで相加平均・相乗平均の不等式を使う.
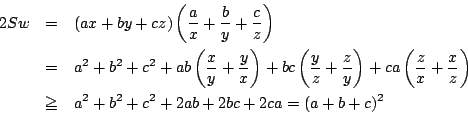
ゆえに ![]() の最小値は
の最小値は
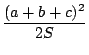 .
.
![]() となるのは
となるのは
![]() の内接円の中心で,
これは確かに
の内接円の中心で,
これは確かに
![]() の内部の点である.
□
の内部の点である.
□